已知a,b为常数,若f(x)=x2+4x+3,f(ax+b)=x2+10x+24,则5a-b= .
【答案】
分析:将ax+b代入函数f(x)的解析式求出f(ax+b),代入已知等式,令等式左右两边的对应项的系数相等,列出方程组,求出a,b的值.
解答:解:由f(x)=x
2+4x+3,f(ax+b)=x
2+10x+24,得
(ax+b)
2+4(ax+b)+3=x
2+10x+24,
即a
2x
2+2abx+b
2+4ax+4b+3=x
2+10x+24.
比较系数得
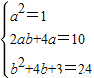
求得a=-1,b=-7,或a=1,b=3,则5a-b=2.
故答案为2
点评:本题考查知f(x)的解析式求f(ax+b)的解析式用代入法.
