
(本题16分,其中第(1)小题8分,第(2)小题8分)
已知椭圆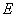 的方程为
的方程为 ,长轴是短轴的2倍,且椭圆
,长轴是短轴的2倍,且椭圆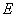 过点
过点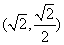 ;斜率为
;斜率为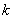 的直线
的直线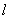 过点
过点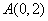 ,
,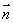 为直线
为直线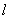 的一个法向量,坐标平面上的点
的一个法向量,坐标平面上的点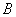 满足条件
满足条件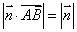 .
.
(1)写出椭圆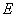 方程,并求点
方程,并求点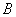 到直线
到直线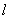 的距离;
的距离;
(2)若椭圆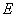 上恰好存在3个这样的点
上恰好存在3个这样的点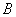 ,求
,求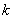 的值.
的值.
解:(1)由题意得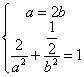 解得
解得 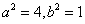 …………3分
…………3分
∴椭圆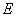 方程为:
方程为: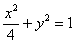 …………4分
…………4分
直线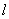 的方程为
的方程为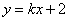 ,其一个法向量
,其一个法向量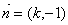 ,设点B的坐标为
,设点B的坐标为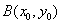 ,由
,由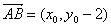 及
及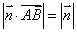 得
得 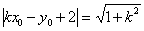 …………6分
…………6分
∴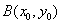 到直线
到直线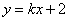 的距离为
的距离为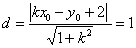 …………8分
…………8分
(2)由(1)知,点B是椭圆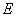 上到直线
上到直线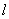 的距离为1的点,即与直线
的距离为1的点,即与直线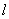 的距离为1的二条平行线与椭圆
的距离为1的二条平行线与椭圆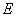 恰好有三个交点。
恰好有三个交点。
设与直线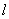 平行的直线方程为
平行的直线方程为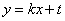
由 得
得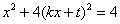 ,即
,即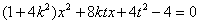
 ………①…………10分
………①…………10分
当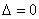 时,
时,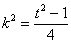 ………②
………②
又由两平行线间的距离为1,可得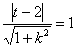 ………③
………③
把②代入③得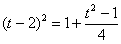 ,即
,即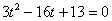 ,
,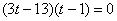
即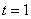 ,或
,或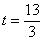 …………12分
…………12分
当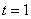 时,代入②得
时,代入②得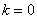 ,代回③得
,代回③得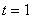 或
或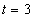
当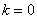 ,
,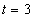 时,由①知
时,由①知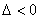
此时两平行线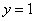 和
和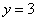 与椭圆
与椭圆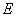 只有一个交点,不合题意;…………14分
只有一个交点,不合题意;…………14分
当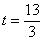 时,代入②得
时,代入②得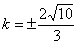 ,代回③得
,代回③得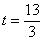 或
或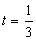
当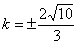 ,
,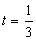 时,由①知
时,由①知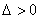
此时两平行线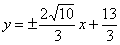 和
和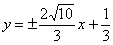 ,与椭圆
,与椭圆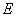 有三个交点,
有三个交点,
∴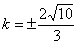 …………16分
…………16分


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2011-2012学年上海市高三模拟考试理科数学 题型:解答题
.(本题满分16分,其中第1小题4分,第2小题6分,第3小题6分,)
如图,已知椭圆 ,
, ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点 为顶点的三角形的周长为
为顶点的三角形的周长为 .一等轴双曲线的顶点是该椭圆的焦点,设
.一等轴双曲线的顶点是该椭圆的焦点,设 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线 和
和 与椭圆的交点分别为
与椭圆的交点分别为 和
和 .
.
(1)求椭圆和双曲线的标准方程;
(2)设直线 、
、 的斜率分别为
的斜率分别为 、
、 ,证明
,证明 ;
;
(3)是否存在常数 ,使得
,使得
恒成立?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分16分,其中第1小题9分,第2小题7分)
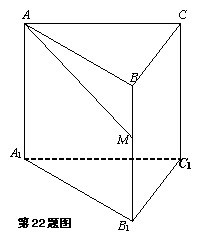
如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为![]() (
(![]() ),动点
),动点![]() 在侧棱
在侧棱![]() 上移动.设
上移动.设![]() 与侧面
与侧面![]() 所成的角为
所成的角为![]() .
.
(1)当![]() 时,求点
时,求点![]() 到平面
到平面![]() 的距离的取值范围;
的距离的取值范围;
 (2)当
(2)当![]() 时,求向量
时,求向量![]() 与
与![]() 夹角的大小.
夹角的大小.
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分16分,其中第1小题3分,第2小题6分,第3小题7分)
设![]() 为非零实数,偶函数
为非零实数,偶函数![]() ,
,![]() .
.
(1) 求实数![]() 的值;
的值;
(2) 试确定函数![]() 的单调区间(不需证明);
的单调区间(不需证明);
(3) 若函数![]() 在区间
在区间![]() 上存在零点,试求实数
上存在零点,试求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010年上海市松江区高考模拟考试(理) 题型:解答题
(本题满分16分,其中第(1)小题4分,第(2)小题8分,第(3)小题4分)
设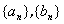 是两个数列,
是两个数列, 为直角坐标平面上的点.对
为直角坐标平面上的点.对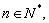 若三点
若三点 共线,
共线,
(1)求数列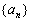 的通项公式;
的通项公式;
(2)若数列{ }满足:
}满足: ,其中
,其中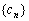 是第三项为8,公比为4的等比数列.求证:点列
是第三项为8,公比为4的等比数列.求证:点列 (1,
(1,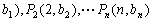 在同一条直线上;
在同一条直线上;
(3)记数列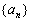 、{
、{ }的前
}的前 项和分别为
项和分别为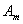 和
和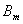 ,对任意自然数
,对任意自然数 ,是否总存在与
,是否总存在与 相关的自然数
相关的自然数 ,使得
,使得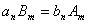 ?若存在,求出
?若存在,求出 与
与 的关系,若不存在,请说明理由.
的关系,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com