
(本题满分16分,其中第1小题3分,第2小题6分,第3小题7分)
设![]() 为非零实数,偶函数
为非零实数,偶函数![]() ,
,![]() .
.
(1) 求实数![]() 的值;
的值;
(2) 试确定函数![]() 的单调区间(不需证明);
的单调区间(不需证明);
(3) 若函数![]() 在区间
在区间![]() 上存在零点,试求实数
上存在零点,试求实数![]() 的取值范围.
的取值范围.
(本题满分16分,理科:第1小题9分,第2小题7分;文科:第1小题3分,第2小题6分,第3小题7分)
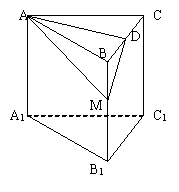
(理科)解:(1)设BC的中点为D,连结AD、DM,则有

![]()
于是,可知![]() 即为AM与侧面BCC1所成角
即为AM与侧面BCC1所成角![]() .
.
因为,点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,不妨设
,不妨设![]() ,
,![]() .
.
在Rt△ADM中,![]() .
.
由![]() ,
,![]() ,故
,故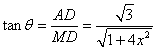 .
.
而当![]() 时,
时,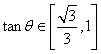 ,
,
即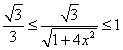
![]() ,
,
所以,点![]() 到平面
到平面![]() 的距离
的距离![]() 的取值范围是
的取值范围是![]() .
.
(2)解法一:当![]() 时,由(1)可知
时,由(1)可知![]() ,
,
故可得![]() ,
,![]() .
.
设向量![]() 与
与![]() 的夹角为
的夹角为![]() ,因为
,因为
![]()
![]() .
.
所以 ,
,
故向量![]() 与
与![]() 夹角的大小为
夹角的大小为![]() .
.
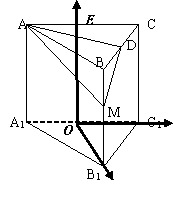
解法二:如图,以![]() 中点O为原点,
中点O为原点,![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴(其中点
轴(其中点![]() 为
为![]() 中点),建立空间直角坐标系.
中点),建立空间直角坐标系.
由(1)可知,当![]() 时,
时,![]() .
.
所以有,![]() ,
,![]() ,
,
![]() ,
,![]() ,即
,即![]() ,
,![]() .
.
设向量![]() 与
与![]() 夹角为
夹角为![]() ,则
,则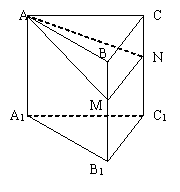
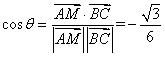
 故向量
故向量![]() 与
与![]() 夹角的大小为
夹角的大小为![]() .
.
解法三:如图,过点![]() 作
作![]() //
//![]() ,交
,交![]() 于
于![]() .
.
联结![]() .因为是正三棱柱,故可得
.因为是正三棱柱,故可得![]() .
.
当![]() 时,由(1)可知
时,由(1)可知![]() ,
,
故可得![]() .
.
在等腰三角形![]() 中,不难求得
中,不难求得
![]() ,即异面直线
,即异面直线![]() 与
与![]() 所成角为
所成角为![]() ,
,
而图中不难发现,![]() 与
与![]() 夹角的大小为异面直线
夹角的大小为异面直线![]() 与
与![]() 所成角的补角,即
所成角的补角,即
![]() 与
与![]() 夹角的大小为
夹角的大小为![]() .
.
![]() 与
与![]() 夹角的大小为
夹角的大小为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2011年江苏省扬州中学高二上学期期中考试数学 题型:解答题
(本题满分16分)如图,设有半径为3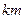 的圆形村落,A、B两人同时从村落中心O出发,B向北直行,A先向东直行,出村后不久,在点P处改变方向,沿着与村落周界相切的直线前进,后来恰与B在点Q处相遇.设A、B两人速度一定,其速度比为3:1,问Q距O多远?
的圆形村落,A、B两人同时从村落中心O出发,B向北直行,A先向东直行,出村后不久,在点P处改变方向,沿着与村落周界相切的直线前进,后来恰与B在点Q处相遇.设A、B两人速度一定,其速度比为3:1,问Q距O多远?
查看答案和解析>>
科目:高中数学 来源:2012-2013学年上海市徐汇区高三上学期期末考试文科数学试卷(解析版) 题型:解答题
(本题满分16分) 本题共有3个小题,第1小题满分4分,第2小题满分6分. 第3小题满分6分.
(文)已知椭圆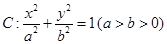 的一个焦点为
的一个焦点为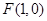 ,点
,点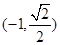 在椭圆
在椭圆 上,点
上,点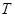 满足
满足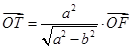 (其中
(其中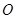 为坐标原点), 过点
为坐标原点), 过点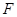 作一斜率为
作一斜率为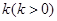 的直线交椭圆于
的直线交椭圆于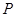 、
、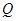 两点(其中
两点(其中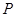 点在
点在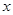 轴上方,
轴上方,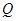 点在
点在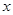 轴下方) .
轴下方) .
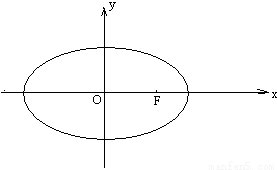
(1)求椭圆 的方程;
的方程;
(2)若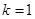 ,求
,求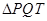 的面积;
的面积;
(3)设点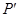 为点
为点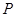 关于
关于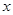 轴的对称点,判断
轴的对称点,判断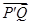 与
与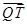 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省无锡市高三上学期期中考试数学(解析版) 题型:解答题
(本题满分16分)
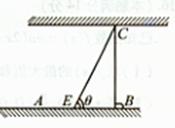
如图为河岸一段的示意图,一游泳者站在河岸的A点处,欲前往河对岸的C点处。若河宽BC为100m,A、B相距100m,他希望尽快到达C,准备从A步行到E(E为河岸AB上的点),再从E游到C。已知此人步行速度为v,游泳速度为0.5v。
(I)设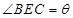 ,试将此人按上述路线从A到C所需时间T表示为
,试将此人按上述路线从A到C所需时间T表示为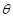 的函数;并求自变量
的函数;并求自变量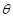 取值范围;
取值范围;
II)当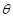 为何值时,此人从A经E游到C所需时间T最小,其最小值是多少?
为何值时,此人从A经E游到C所需时间T最小,其最小值是多少?
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省无锡市高三第二次考试文科数学试卷 题型:解答题
(本题满分16分)
已知数列 ,其前
,其前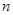 项和为
项和为 ,对任意
,对任意 都有:
都有:
(1)求证: 是等比数列;
是等比数列;
(2)若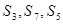 构成等差数列,求实数
构成等差数列,求实数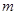 的值;
的值;
(3)求证:对任意大于1的实数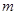 ,
,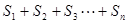 ,
,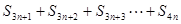 ,
,
 不能构成等差数列.
不能构成等差数列.
查看答案和解析>>
科目:高中数学 来源:2011年江苏省高二上学期期中考试数学 题型:解答题
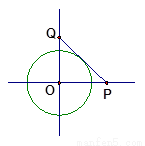
(本题满分16分)如图,设有半径为3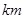 的圆形村落,A、B两人同时从村落中心O出发,B向北直行,A先向东直行,出村后不久,在点P处改变方向,沿着与村落周界相切的直线前进,后来恰与B在点Q处相遇.设A、B两人速度一定,其速度比为3:1,问Q距O多远?
的圆形村落,A、B两人同时从村落中心O出发,B向北直行,A先向东直行,出村后不久,在点P处改变方向,沿着与村落周界相切的直线前进,后来恰与B在点Q处相遇.设A、B两人速度一定,其速度比为3:1,问Q距O多远?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com