练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，三棱柱的底面是等边三角形，在底面ABC上的射影为的重心G.

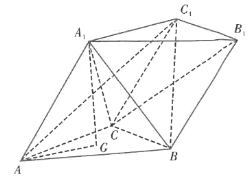
    （1）已知，证明：平面平面；

    （2）若三棱柱的侧棱与底面所成角的正切值为，，求点到平面的距离.

    【答案】（1）证明见详解，（2）.

    【解析】

    （1）先证明和，然后得出平面即可

    （2）由条件算出，，，，，然后利用求解即可.

    （1）连结并延长交于

    由已知得平面，且

    所以，因为，所以平面

    所以

    因为四边形是平行四边形，且

    所以四边形是菱形，所以

    因为，所以平面

    因为平面，所以平面平面

    （2）因为平面，所以侧棱与底面所成的角为

    即

    因为，所以，

    因为在底面ABC上的射影为的重心G，

    所以等边三角形的边长

    同理，在直角三角形中，

    因为在底面ABC上的射影为的重心G，

    所以，且

    因为，所以平面

    所以，因为，所以

    所以在直角三角形中，

    因为，所以为直角三角形

    设点到平面的距离为，由得

    ，所以可得

    即点到平面的距离为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的内接等边三角形的面积为（其中为坐标原点）．

    （1）试求抛物线的方程；

    （2）已知点两点在抛物线上，是以点为直角顶点的直角三角形．

    ①求证：直线恒过定点；

    ②过点作直线的垂线交于点，试求点的轨迹方程，并说明其轨迹是何种曲线．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，以原点为极点，轴非负半轴为极轴，长度单位相同，建立极坐标系，曲线的极坐标方程为，直线过点倾斜角为.

    （1）将曲线的极坐标方程化为直角坐标方程，并写出直线的参数方程；

    （2）当时，直线交曲线于，两点，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】图1是矩形，，，M为的中点，将沿翻折，得到四棱锥，如图2．

    （Ⅰ）若点N为的中点，求证：平面；

    （Ⅱ）若．求点A到平面的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四边形中，，以为折痕把折起，使点到达点的位置，且.

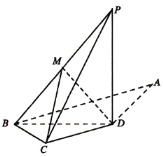
    （1）证明：平面；

    （2）若为的中点，二面角等于60°，求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点，直线：，点为上一动点，过作直线，为的中垂线，与交于点，设点的轨迹为曲线Γ.

    （1）求曲线Γ的方程；

    （2）若过的直线与Γ交于两点，线段的垂直平分线交轴于点，求与的比值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校周五的课程表设计中，要求安排8节课（上午4节下午4节），分别安排语文数学英语物理化学生物政治历史各一节，其中生物只能安排在第一节或最后一节，数学和英语在安排时必须相邻（注：上午的最后一节与下午的第一节不记作相邻），则周五的课程顺序的编排方法共有（ ）．

    A.4800种B.2400种C.1200种D.240种

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设，函数.

    （Ⅰ）讨论函数在定义域上的单调性；

    （Ⅱ）若函数的图象在点处的切线与直线平行，且对任意，，不等式恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系，曲线的参数方程为（为参数），以坐标原点为极点，轴的正半轴为极轴，取相同长度单位建立极坐标系，直线的极坐标方程为

    （1）求曲线的普通方程和直线的直角坐标方程；

    （2）设直线与轴的交点为，经过点的动直线与曲线交于，两点，证明：为定值

    查看答案和解析>>

    同步练习册答案