练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．某几何体的三视图（单位：cm）如图，则这个几何体的表面积为（单位：cm2）（　　）
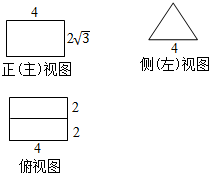
    A．24+4$\sqrt{3}$B．48+8$\sqrt{3}$C．24+8$\sqrt{3}$D．48+4$\sqrt{3}$

    分析 几何体为侧放的直三棱柱，棱柱的底面为侧视图三角形，棱柱的高为4．

    解答 解：由三视图可知几何体为侧放的直三棱柱，棱柱的底面为侧视图中的等边三角形，棱柱的高为4．
    ∴棱柱的表面积S=$\frac{1}{2}×4×2\sqrt{3}×2$+3×4×4=48+8$\sqrt{3}$．
    故选B．

    点评 本题考查了棱柱的三视图，表面积计算，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．在数列{an}中，a1=1，an+1=2an，Sn为{an}的前n项和，则S5=（　　）
    A．-30B．31C．-32D．33

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．设p：y=cx是R上的单调递减函数；q：函数g（x）=lg（2cx2+2x+1）的值域为R．如果“p且q”为假命题，“p或q”为真命题，则正实数c的取值范围是（　　）
    A．$（{\frac{1}{2}，1}）$B．$（{\frac{1}{2}，+∞}）$C．$（{0，\frac{1}{2}}]∪[{1，+∞}）$D．$（{0，\frac{1}{2}}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．若函数f（x）是定义域为R，最小正周期为π的函数，且当x∈[0，π]时，当f（x）=sinx，则$f（\frac{15π}{4}）$=$\frac{\sqrt{2}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．下列叙述中正确的是（　　）
    A．“m=2”是“l1：2x+（m+1）y+4=0与l2：mx+3y-2=0平行”的充分条件
    B．“方程Ax2+By2=1表示椭圆”的充要条件是“A≠B”
    C．命题“?x∈R，x2≥0”的否定是“?x0∈R，x02≥0”
    D．命题“a、b都是偶数，则a+b是偶数”的逆否命题为“a+b不是偶数，则a、b都是奇数”

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．设函数f（x）=$\left\{\begin{array}{l}{{2}^{1-x}，x≤1}\\{1-lo{g}_{2}x，x＞1}\end{array}\right.$，则不等式f（x）≤2的解集为（　　）
    A．（0，1]∪（2，+∞）B．[0，+∞）C．[0，1]D．（0，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．若关于x的方程x3-3x-m=0在[0，2]上有根，则实数m的取值范围是（　　）
    A．[-2，2]B．[0，2]C．[-2，0]D．（-∞，-2）∪（2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．下列说法不正确的是（　　）
    A．a∥b，a?α，b⊆α⇒a∥αB．α∥β，b∥β，a，b⊆α⇒α∥β
    C．a⊥b，a⊥c，b∩c=p，p∈α，a?α⇒a⊥αD．α⊥β，α∩β=l，b⊆α，b⊥l⇒b⊥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．下列有关命题的说法错误的个数是（　　）
    ①命题“若x2=1，则x=1”的否命题为“若x2=1，则x≠1”
    ②“x=-1”是“x2-5x-6=0”的充分不必要条件
    ③命题“存在x∈R，使得x2+x-1＜0”的否定是：“任意x∈R，均有x2+x-1＞0”
    ④命题“若x=y，则sin x=sin y”的逆否命题为真命题
    ⑤若“p或q”为真命题，则p、q均为真命题．
    A．2B．3C．4D．5

    查看答案和解析>>

    同步练习册答案