
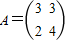 ,向量
,向量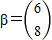 ,
,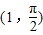 ,曲线C的参数方程为
,曲线C的参数方程为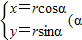 为参数,r>0)
为参数,r>0)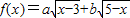 的最大值,以及取得最大值时x的值.
的最大值,以及取得最大值时x的值.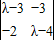 =λ2-7λ+6,令f(λ)=0,能求出矩阵M的特征值和特征向量.
=λ2-7λ+6,令f(λ)=0,能求出矩阵M的特征值和特征向量.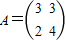 ,知A2=
,知A2= ,设向量α=
,设向量α= ,由向量
,由向量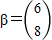 ,A2α=β,能求出向量α.
,A2α=β,能求出向量α.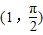 ,求出A,B的普通方程,由此能直线AB的直角坐标方程.
,求出A,B的普通方程,由此能直线AB的直角坐标方程.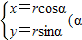 为参数,r>0),知曲线C的普通方程为x2+y2=r2.再由直线AB和曲线C只有一个交点,能求出r.
为参数,r>0),知曲线C的普通方程为x2+y2=r2.再由直线AB和曲线C只有一个交点,能求出r.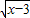 +3
+3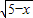 ,3≤x≤5.由(4
,3≤x≤5.由(4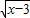 +3
+3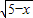 )2=7x-3+24
)2=7x-3+24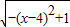 ,由此能求出f(x)的最大值为和此时x值.
,由此能求出f(x)的最大值为和此时x值.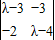 =λ2-7λ+6,
=λ2-7λ+6,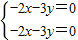 ,解得2x+3y=0
,解得2x+3y=0 .
.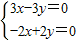 ,解得x=y
,解得x=y .
. ,∴
,∴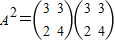 =
= ,
, ,∵
,∵ ,向量
,向量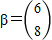 ,A2α=β,
,A2α=β,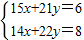 ,解得x=-1,y=1,
,解得x=-1,y=1,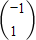 .
.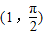 ,
,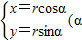 为参数,r>0),
为参数,r>0), =r,解得r=
=r,解得r=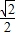 .
.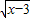 +3
+3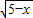 ,3≤x≤5.
,3≤x≤5.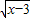 +3
+3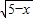 )2=16x-48+45-9x+24
)2=16x-48+45-9x+24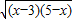
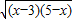
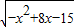
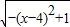


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
|
|
| 1 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
| π |
| 2 |
|
| x-3 |
| 5-x |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省苏州市木渎高级中学天华学校高三(上)12月月考数学试卷(解析版) 题型:解答题
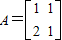 ,向量
,向量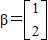 .求向量α,使得A2α=β.
.求向量α,使得A2α=β. ,点P(x,y)是椭圆上的点,若
,点P(x,y)是椭圆上的点,若 的最大值为10,求椭圆的标准方程.
的最大值为10,求椭圆的标准方程.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省苏州市木渎高级中学天华学校高三(上)12月月考数学试卷(解析版) 题型:解答题
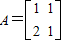 ,向量
,向量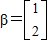 .求向量α,使得A2α=β.
.求向量α,使得A2α=β. ,点P(x,y)是椭圆上的点,若
,点P(x,y)是椭圆上的点,若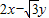 的最大值为10,求椭圆的标准方程.
的最大值为10,求椭圆的标准方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com