
【题目】设函数f(x)= ![]() ,(a∈R)
,(a∈R)
(1)若f(x)在x=0处取得极值,确定a的值.
(2)若f(x)在R上为增函数,求a的取值范围.
【答案】
(1)解:函数f(x)= ![]() ,
,
可得f′(x)= ![]() .
.
由f(x)在x=0处取得极值得f′(0)=0,解得a=1
(2)解:由(1)得f′(x)= ![]() ,因为f(x)在R上增函数,
,因为f(x)在R上增函数,
∴f′(x)≥0恒成立,即cosx﹣sinx≥a恒成立,
∴ ![]() sin(
sin( ![]() ﹣x)≥a恒成立,
﹣x)≥a恒成立,
∴a≤﹣ ![]() .
.
【解析】(1)求出函数的导数,利用函数的极值,转化求解a即可.(2)利用函数的单调性,推出不等式,然后求解a的范围即可.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减),还要掌握函数的极值与导数(求函数
在这个区间单调递减),还要掌握函数的极值与导数(求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值)的相关知识才是答题的关键.
是极小值)的相关知识才是答题的关键.


科目:高中数学 来源: 题型:
【题目】已知直线l经过直线l1:2x﹣y﹣1=0与直线l2:x+2y﹣3=0的交点P,且与直线l3:x﹣y+1=0垂直.
(1)求直线l的方程;
(2)若直线l与圆C:(x﹣a)2+y2=8相交于P,Q两点,且 ![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点(1,﹣2)和( ![]() ,0)在直线l:ax﹣y﹣1=0(a≠0)的两侧,则直线l的倾斜角的取值范围是( )
,0)在直线l:ax﹣y﹣1=0(a≠0)的两侧,则直线l的倾斜角的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.(0, ![]() )∪(
)∪( ![]() ,π)
,π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线y2=4x的焦点为F,过点(0,3)的直线与抛物线交于A,B两点,线段AB的垂直平分线交x轴于点D,若|AF|+|BF|=6,则点D的横坐标为 . 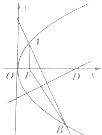
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x﹣8,g(x)=2x2﹣4x﹣16,
(1)求不等式g(x)<0的解集;
(2)若对一切x>5,均有f(x)≥(m+2)x﹣m﹣15成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com