
在棱长为2的正方体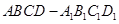 中,设
中,设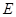 是棱
是棱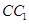 的中点.
的中点.
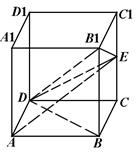
⑴ 求证: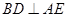 ;
;
⑵ 求证: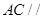 平面
平面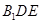 ;
;
⑶ 求三棱锥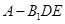 的体积.
的体积.
⑴连接BD,AE. 故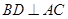 ,因
,因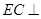 底面ABCD,故
底面ABCD,故 ,故
,故 平面
平面 故
故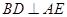 ⑵连接
⑵连接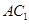 ,设
,设 ,连接
,连接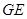 ,则
,则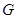 为
为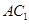 中点,而
中点,而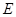 为
为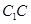 的中点,则
的中点,则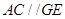 故
故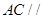 平面
平面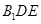 ⑶
⑶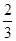
【解析】
试题分析:(1)连接BD,AE. 因四边形ABCD为正方形,故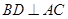 ,
, 
因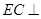 底面ABCD,
底面ABCD,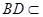 面ABCD,故
面ABCD,故 ,又
,又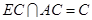 ,
,
故 平面
平面 ,
,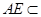 平面
平面 ,故
,故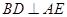 .
.
⑵. 连接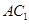 ,设
,设 ,连接
,连接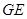 ,
,
则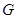 为
为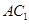 中点,而
中点,而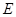 为
为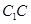 的中点,故
的中点,故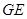 为三角形
为三角形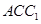 的中位线,
的中位线,
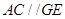 ,
,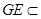 平面
平面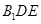 ,
,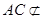 平面
平面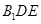 ,故
,故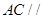 平面
平面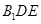 .
.
⑶. 由⑵知,点A到平面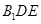 的距离等于C到平面
的距离等于C到平面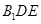 的距离,故三棱锥
的距离,故三棱锥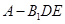 的体积
的体积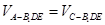 ,而
,而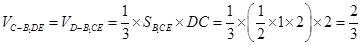 ,三棱锥
,三棱锥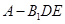 的体积为
的体积为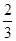 .
.
考点:线面平行垂直的判定与性质及锥体的体积
点评:要证明线面平行常借助于平面外一直线与平面内一直线平行;线面的垂直关系中常用的思路是线线垂直与线面垂直的互相转化;第三问求三棱锥体积时采用等体积法的思路转化底面和顶点,是底面积和高都容易求出


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
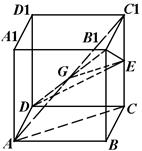
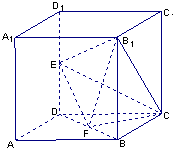 如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点.
如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点. 查看答案和解析>>
科目:高中数学 来源:2012-2013学年内蒙古高三5月月考理科数学试卷(解析版) 题型:选择题
在棱长为2的正方体中,点E,F分别是棱AB,BC的中点,则点 到平面
到平面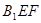 的距离等于( )
的距离等于( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三高考压轴数学试卷(解析版) 题型:填空题
在棱长为2的正方体 中,点
中,点 为底面
为底面 的中心,在正方体
的中心,在正方体 内随机取一点
内随机取一点 ,则点
,则点 到点
到点 的距离大于1的概率为
的距离大于1的概率为
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河北省高三高考仿真文数 题型:选择题
.在棱长为2的正方体 中,动点
中,动点 在
在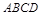 内,且到直线
内,且到直线 的距离之和等于
的距离之和等于 ,则
,则 的面积最大值是 ( )
的面积最大值是 ( )
A. B.1 C.2 D.4
B.1 C.2 D.4
查看答案和解析>>
科目:高中数学 来源:2012届辽宁省营口市高二上学期期末教学质量检测理科数学 题型:选择题
如图,在棱长为2的正方体 中,
中,
 为底面的中心,
为底面的中心, 是
是 的中点,那么异面直线
的中点,那么异面直线
 与
与 所成角的余弦值为
所成角的余弦值为
(A)  (B)
(B)  (C)
(C)  (D)
(D)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com