用长为90cm，宽为48cm的长方形铁皮做一个无盖的容器，先在四角分别截去一个小正方形，然后把四边翻转90°角，再焊接而成（如图），问该容器的高为多少时，容器的容积最大？最大容积是多少？
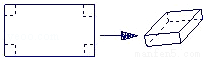
当高为10，最大容积为19600．
【解析】
试题分析：首先分析题目求长为90cm，宽为48cm的长方形铁皮做一个无盖的容器当容器的高为多少时，容器的容积最大．故可设容器的高为x，体积为V，求出v关于x的方程，然后求出导函数，分析单调性即可求得最值．
【解析】
根据题意可设容器的高为x，容器的体积为V，
则有V=（90﹣2x）（48﹣2x）x=4x3﹣276x2+4320x，（0＜x＜24）
求导可得到：V′=12x2﹣552x+4320
由V′=12x2﹣552x+4320=0得x1=10，x2=36．
所以当x＜10时，V′＞0，
当10＜x＜36时，V′＜0，
当x＞36时，V′＞0，
所以，当x=10，V有极大值V（10）=19600，又V（0）=0，V（24）=0，
所以当x=10，V有最大值V（10）=19600
故答案为当高为10，最大容积为19600．
科目：高中数学 来源：[同步]2014年苏教版必修二 2.3空间直角坐标系练习卷（解析版） 题型：解答题
已知空间直角坐标系O﹣xyz中的点A（1，1，1），平面α过点A且与直线OA垂直，动点P（x，y，z）是平面α内的任一点．
（1）求点P的坐标满足的条件；
（2）求平面α与坐标平面围成的几何体的体积．
查看答案和解析>>
科目：高中数学 来源：[同步]2014年苏教版必修一 1.2 子集、全集、补集练习卷（解析版） 题型：解答题
已知a∈R，b∈R，A={2，4，x2﹣5x+9}，B={3，x2+ax+a}，C={x2+（a+1）x﹣3，1}：求
（1）A={2，3，4}的x值；
（2）使2∈B，B?A，求a，x的值；
（3）使B=C的a，x的值．
查看答案和解析>>
科目：高中数学 来源：[同步]2014年苏教版必修一 1.2 子集、全集、补集练习卷（解析版） 题型：选择题
下列各式中，正确的个数是（ ）
①ϕ={0}；②ϕ⊆{0}；③ϕ∈{0}；④0={0}；⑤0∈{0}；⑥{1}∈{1，2，3}；⑦{1，2}⊆{1，2，3}；⑧{a，b}⊆{b，a}．
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目：高中数学 来源：[同步]2014年湘教版选修1-1 3.4 生活中的优化问题举例练习卷（解析版） 题型：填空题
设底为等边三角形的直棱柱的体积为V，那么其表面积最小时，底面边长为 ．
查看答案和解析>>
科目：高中数学 来源：[同步]2014年湘教版选修1-1 3.4 生活中的优化问题举例练习卷（解析版） 题型：填空题
某商品一件的成本为30元，在某段时间内，若以每件x元出售，可卖出（200﹣x）件，当每件商品的定价为 元时，利润最大．
查看答案和解析>>
科目：高中数学 来源：[同步]2014年湘教版选修1-1 3.2导数的运算练习卷（解析版） 题型：解答题
已知P（﹣1，1），Q（2，4）是曲线y=x2上的两点，求与直线PQ平行且与曲线相切的切线方程．
查看答案和解析>>
科目：高中数学 来源：[同步]2014年湘教版选修1-1 2.4 圆锥曲线的应用练习卷（解析版） 题型：填空题
（5分）河上有一抛物线型拱桥，当水面距拱顶5 m时，水面宽为8 m，一小船宽4 m，高2 m，载货后船露出水面上的部分高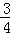
m，问水面上涨到与抛物线拱顶相距 m时，小船不能通航．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com