
用总长为14.8m的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积最大?并求出它的最大容积.
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源:2015届河南省濮阳市高二下学期升级考试理科试卷(A卷)(解析版) 题型:解答题
在平面直角坐标系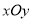 中,动点
中,动点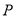 到两点
到两点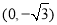 、
、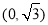 的距离之和等于4.设点
的距离之和等于4.设点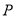 的轨迹为
的轨迹为 .
.
(1)求曲线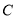 的方程;
的方程;
(2)设直线 与
与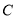 交于
交于 、
、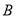 两点,若
两点,若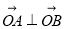 ,求
,求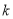 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2015届河南省濮阳市高二下学期升级考试理科数学试卷(A)(解析版) 题型:选择题
在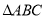 中,若
中,若 ,则
,则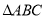 的形状是 ( )
的形状是 ( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.不能确定
查看答案和解析>>
科目:高中数学 来源:2015届河南省濮阳市高二下学期升级考试文科试卷(A卷)(解析版) 题型:选择题
用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,假设正确的是( )
A.假设三内角都不大于60度
B.假设三内角都大于60度
C.假设三内危至多有一个大于60度
D.假设三内角至多有两个大于60度
查看答案和解析>>
科目:高中数学 来源:2015届河南省濮阳市高二下学期升级考试文科数学试卷(A)(解析版) 题型:填空题
已知双曲线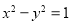 ,点
,点 为其两个焦点,点P为双曲线上一点,若
为其两个焦点,点P为双曲线上一点,若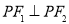 ,则
,则 的值为__________.
的值为__________.
查看答案和解析>>
科目:高中数学 来源:2015届河南省高二下学期第一次月考理科数学试卷(解析版) 题型:选择题
函数 的定义域为开区间
的定义域为开区间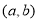 ,导函数
,导函数 在
在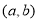 内的图像如图所示,则函数
内的图像如图所示,则函数 在开区间
在开区间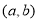 内有极小值点( )
内有极小值点( )

A.1个 B. 个 C.
个 C. 个 D.
个 D. 个
个
查看答案和解析>>
科目:高中数学 来源:2015届河南省高二普通班上学期期中理科数学试卷(解析版) 题型:选择题
若{an}为等差数列,Sn为其前n项和,若首项 ,公差
,公差 ,则使Sn最大的序号n为( )
,则使Sn最大的序号n为( )
A.2 B.3 C.4 D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com