
分析 (1)根据函数奇偶性和单调性的定义进行证明即可.
(2)根据函数奇偶性和单调性的关系将不等式进行转化求解即可.
解答 解:(1)∵f(-x)=$\frac{a}{a-1}$(2-x-2x)=-$\frac{a}{a-1}$(2x-2-x)=-f(x),
∴f(x)为奇函数.…(2分)
设x1<x2,f(x1)-f(x2)=$\frac{a}{a-1}$(${2}^{{x}_{1}}$-$\frac{1}{{2}^{{x}_{1}}}$-${2}^{{x}_{2}}$+$\frac{1}{{2}^{{x}_{2}}}$)=$\frac{a}{a-1}$(${2}^{{x}_{1}}$-${2}^{{x}_{2}}$)(1+$\frac{1}{{2}^{{x}_{1}+{x}_{2}}}$),
∵y=2x是增函数,∴${2}^{{x}_{1}}$-${2}^{{x}_{2}}$<0,又1+$\frac{1}{{2}^{{x}_{1}+{x}_{2}}}$>0,
∴当0<a<1时,f(x1)-f(x2)>0,即f(x1)>f(x2),函数f(x)是减函数
当a>1时,f(x1)-f(x2)<0,即f(x1)<f(x2),函数f(x)是增函数.…(6分)
(2)由f(m-1)+f(m)<0得f(m)<-f(m-1)
由(1)知f(x)为奇函数,∴f(m)<f(1-m) …(8分)
又由(1)得
当0<a<1时,函数f(x)是减函数
∴$\left\{\begin{array}{l}{m>1-m}\\{-1<m<1}\\{-1<1-m<1}\end{array}\right.$解得$\frac{1}{2}$<m<1 …(10分)
当a>1时,函数f(x)是增函数
∴$\left\{\begin{array}{l}{m<1-m}\\{-1<m<1}\\{-1<1-m<1}\end{array}\right.$,解得0<m<$\frac{1}{2}$.…(12分)
点评 本题主要考查函数奇偶性和单调性的判断和应用,利用函数奇偶性和单调性的定义进行证明和转化是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤3} | B. | {x|2<x<3} | C. | {x|-1≤x≤3} | D. | R |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{2}$ | B. | 7 | C. | -1或7 | D. | -$\frac{1}{2}$或$\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<2} | B. | {x|1<x<2} | C. | {x|x>0} | D. | {x|x≥1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
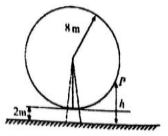 如图,一个摩天轮的半径为8m,每12min旋转一周,最低点离地面为2m,若摩天轮边缘某点P从最低点按逆时针方向开始旋转,则点P离地面的距离h(m)与时间t(min)之间的函数关系是( )
如图,一个摩天轮的半径为8m,每12min旋转一周,最低点离地面为2m,若摩天轮边缘某点P从最低点按逆时针方向开始旋转,则点P离地面的距离h(m)与时间t(min)之间的函数关系是( )| A. | h=8cost+10 | B. | h=-8cos$\frac{π}{3}$t+10 | C. | h=-8sin$\frac{π}{6}$t+10 | D. | h=-8cos$\frac{π}{6}$t+10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com