解:(I)∵向量
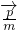
=(sin(A-B),sin(

-A)),
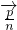
=(1,2sinB),
∴
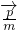
•
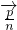
=sin(A-B)+2sin(

-A)sinB=-sin2C,
即sinAcosB-cosAsinB+2cosAsinB=sin2C,
可得sin(A+B)=-2sinCcosC
∵A+B=π-C,可得sin(A+B)=sinC
∴sinC=-2sinCcosC,结合sinC>0可得cosC=-

∵C∈(0,π),∴C=

,即角C的大小为

;
(II)∵S
△ABC=

absinC=

,且C=

,∴ab=4
由余弦定理,得c
2=a
2+b
2-2abcos

=(a+b)
2-ab
∵sinA+sinB=2sinC,∴根据正弦定理,得a+b=2c,
由此可得:c
2=(a+b)
2-ab=4c
2-4,得3c
2=4,解之得c=

.
分析:(I)根据平面向量的坐标运算公式,可得sin(A-B)+2sin(

-A)sinB=-sin2C,利用诱导公式和两角和与差的正弦公式化简得sin(A+B)=-2sinCcosC,结合sin(A+B)=sinC算出cosC=-

,从而得到角C的大小为

;
(II)根据正弦定理的面积公式,结合已知条件算出ab=4,再利用余弦定理算出c
2=(a+b)
2-ab.而由sinA+sinB=2sinC结合正弦定理得a+b=2c,从而得到关于c的方程,解之即可得到边c=

.
点评:本题给出向量含有三角函数的坐标形式,在已知数量积的情况下求角C的大小并依此解三角形,着重考查了平面向量数量积运算公式和运用正余弦定理解三角形等知识,属于中档题.

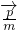 =(sin(A-B),sin(
=(sin(A-B),sin( -A)),
-A)),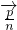 =(1,2sinB),
=(1,2sinB),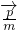 •
•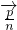 =-sin2C,其中A,B,C分别为△ABC的三边a,b,c所对的角.
=-sin2C,其中A,B,C分别为△ABC的三边a,b,c所对的角. ,求边c的长.
,求边c的长.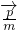 =(sin(A-B),sin(
=(sin(A-B),sin( -A)),
-A)),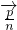 =(1,2sinB),
=(1,2sinB),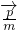 •
•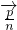 =sin(A-B)+2sin(
=sin(A-B)+2sin( -A)sinB=-sin2C,
-A)sinB=-sin2C,
 ,即角C的大小为
,即角C的大小为 ;
; absinC=
absinC= ,且C=
,且C= ,∴ab=4
,∴ab=4 =(a+b)2-ab
=(a+b)2-ab .
. -A)sinB=-sin2C,利用诱导公式和两角和与差的正弦公式化简得sin(A+B)=-2sinCcosC,结合sin(A+B)=sinC算出cosC=-
-A)sinB=-sin2C,利用诱导公式和两角和与差的正弦公式化简得sin(A+B)=-2sinCcosC,结合sin(A+B)=sinC算出cosC=- ,从而得到角C的大小为
,从而得到角C的大小为 ;
; .
.
