
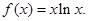 (I)求函数
(I)求函数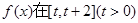 上的最小值;(II)求证:对一切
上的最小值;(II)求证:对一切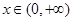 ,都有
,都有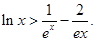
 ),f ′(x)<0,f (x)单调递减,
),f ′(x)<0,f (x)单调递减, ,+∞),f ′(x)>0,f (x)单调递增. ……2分
,+∞),f ′(x)>0,f (x)单调递增. ……2分 ,t无解;②0<t<
,t无解;②0<t< <t+2,即0<t<
<t+2,即0<t< 时,f (x)min=f (
时,f (x)min=f ( )=-
)=- ;
; ≤t<t+2,即t≥
≤t<t+2,即t≥ 时,f (x)在[t,t+2]上单调递增,f (x)min=f (t)=tlnt;
时,f (x)在[t,t+2]上单调递增,f (x)min=f (t)=tlnt;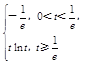 . ……6分
. ……6分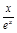 -
-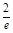 (x∈(0,+∞)),
(x∈(0,+∞)), ,当且仅当x=
,当且仅当x= 时取到.
时取到.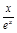 -
-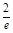 (x∈(0,+∞)),则m ′(x)=
(x∈(0,+∞)),则m ′(x)=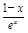 ,易得m (x)max=m (1)=-
,易得m (x)max=m (1)=- ,当且仅当x=1时取到,从而对一切x∈(0,+∞),都有lnx>
,当且仅当x=1时取到,从而对一切x∈(0,+∞),都有lnx>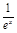 -
-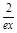 .…12分
.…12分

科目:高中数学 来源:不详 题型:解答题
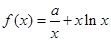 ,
, 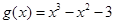 .
.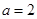 时,求曲线
时,求曲线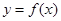 在
在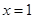 处的切线方程;
处的切线方程;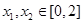 ,使得
,使得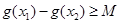 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数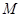 ;
;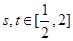 ,都有
,都有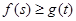 成立,求实数
成立,求实数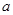 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
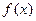 =
=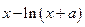 在
在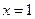 处取得极值.
处取得极值.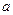 的值;
的值;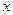 的方程
的方程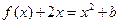 在
在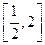 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数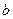 的取值范围;
的取值范围;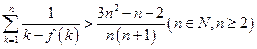 .参考数据:
.参考数据: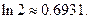
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
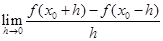 =( )
=( )| A.f ′(x0) | B.2f′(x0) | C.-2f′(x0) | D.0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com