
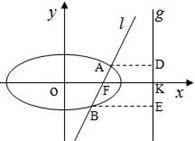
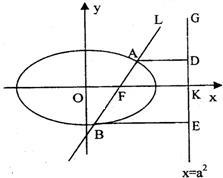
如图,已知直线l:x=my+1过椭圆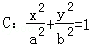 的右焦点F,抛物线:
的右焦点F,抛物线: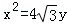 的焦点为椭圆C的上顶点,且直线l交椭圆C于A、B两点,点A、F、B在直线g:x=4上的射影依次为点D、K、E.(1)椭圆C的方程;(2)直线l交y轴于点M,且
的焦点为椭圆C的上顶点,且直线l交椭圆C于A、B两点,点A、F、B在直线g:x=4上的射影依次为点D、K、E.(1)椭圆C的方程;(2)直线l交y轴于点M,且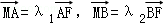 ,当m变化时,探求λ1+λ2的值是否为定值?若是,求出λ1+λ2的值,否则,说明理由;(3)接AE、BD,试证明当m变化时,直线AE与BD相交于定点
,当m变化时,探求λ1+λ2的值是否为定值?若是,求出λ1+λ2的值,否则,说明理由;(3)接AE、BD,试证明当m变化时,直线AE与BD相交于定点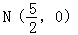 .
.
(1)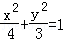
(2) 当m变化时,λ1+λ2的值为定值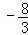 ;
;
(3)当m变化时,AE与BD相交于定点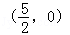
【解析】
试题分析:(1)知椭圆右焦点F(1,0),∴c=1,
抛物线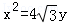 的焦点坐标
的焦点坐标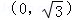 ,∴
,∴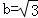 ∴b2=3
∴b2=3
∴a2=b2+c2=4∴椭圆C的方程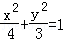 4分
4分
(2)知m≠0,且l与y轴交于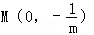 ,
,
设直线l交椭圆于A(x1,y1),B(x2,y2)
由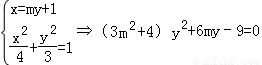 -
5分
-
5分
∴△=(6m)2+36(3m2+4)=144(m2+1)>0
∴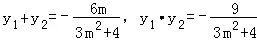 6分
6分
又由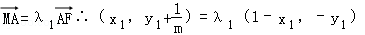
∴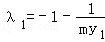
同理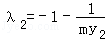 -
7分
-
7分
∴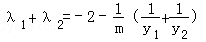
∵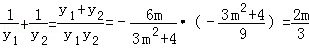
∴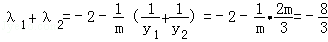
所以,当m变化时,λ1+λ2的值为定值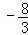 ; 9分
; 9分
(3):由(2)A(x1,y1),B(x2,y2),∴D(4,y1),E(4,y2)
方法1)∵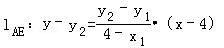 10分
10分
当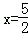 时,
时,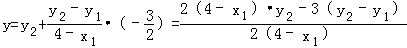 =
=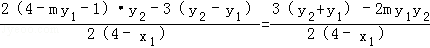
=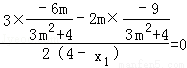 12分
12分
∴点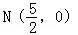 在直线lAE上, 13分
在直线lAE上, 13分
同理可证,点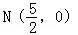 也在直线lBD上;
也在直线lBD上;
∴当m变化时,AE与BD相交于定点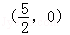 14分
14分
方法2)∵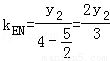 10分
10分
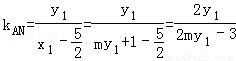 -
11分
-
11分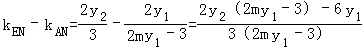
=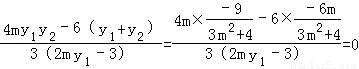 12分
12分
∴kEN=kAN∴A、N、E三点共线,
同理可得B、N、D也三点共线; 13分
∴当m变化时,AE与BD相交于定点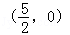 . 14分
. 14分
考点:椭圆的方程,直线与椭圆的位置关系
点评:解决的关键是对于椭圆的几何性质的表示,以及联立方程组的思想结合韦达定理来求解,属于基础题。


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
 如图,已知直线l:x=my+1过椭圆C:
如图,已知直线l:x=my+1过椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| MA |
| AF |
| MB |
| BF |
| 5 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知直线l:x=my+4(m∈R)与x轴交于点P,交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,记直线AQ,BQ的斜率分别为k1,k2.
如图,已知直线l:x=my+4(m∈R)与x轴交于点P,交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,记直线AQ,BQ的斜率分别为k1,k2.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知直线L:x=my+1过椭圆C:
如图,已知直线L:x=my+1过椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•乐山二模)如图,已知直线L:x=my+1过椭圆C:
(2012•乐山二模)如图,已知直线L:x=my+1过椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| MA |
| AF |
| MB |
| BF |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知直线L:x=my+1过椭圆C:
如图,已知直线L:x=my+1过椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| a2+1 |
| 2 |
| AN |
| NE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com