【答案】
分析:(1)根据曲线的解析式求出导函数,把P的横坐标代入导函数中即可求出切线的斜率,根据P的坐标和求出的斜率写出切线的方程即可;
(2)设出曲线过点P切线方程的切点坐标,把切点的横坐标代入到(1)求出的导函数中即可表示出切线的斜率,根据切点坐标和表示出的斜率,写出切线的方程,把P的坐标代入切线方程即可得到关于切点横坐标的方程,求出方程的解即可得到切点横坐标的值,分别代入所设的切线方程即可.
解答:解:(1)∵P(2,4)在曲线 y=

x
3+

上,且y'=x
2∴在点P(2,4)处的切线的斜率k=y'|
x=2=4;
∴曲线在点P(2,4)处的切线方程为y-4=4(x-2),即4x-y-4=0.
(2)设曲线 y=

x
3+

与过点P(2,4)的切线相切于点A(x
,

x
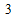
+

),
则切线的斜率 k=y′|x=x0=x02,
∴切线方程为y-(

x
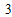
+

)=x
2(x-x
),
即 y=x
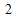
•x-

x
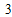
+

,
∵点P(2,4)在切线上,
∴4=2x
2-

x
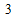
+

,
即x
3-3x
2+4=0,
∴x
3+x
2-4x
2+4=0,
∴(x
+1)(x
-2)
2=0
解得x
=-1或x
=2
故所求的切线方程为4x-y-4=0或x-y+2=0.
点评:此题考查学生会利用导数研究曲线上某点的切线方程,是一道综合题.学生在解决此类问题一定要分清“在某点处的切线”,还是“过某点的切线”;同时解决“过某点的切线”问题,一般是设出切点坐标解决.

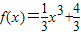 ,
, x3+
x3+ 上,且y'=x2
上,且y'=x2 x3+
x3+ 与过点P(2,4)的切线相切于点A(x,
与过点P(2,4)的切线相切于点A(x, x
x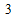 +
+ ),
), x
x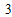 +
+ )=x2(x-x),
)=x2(x-x), •x-
•x- x
x +
+ ,
, x
x +
+ ,
,

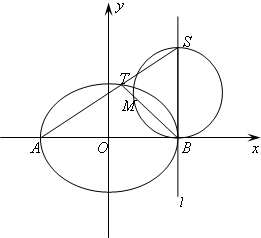 如图,已知曲线C:
如图,已知曲线C: