
【题目】关于x的方程 ![]() (a>0,且a≠1)解的个数是( )
(a>0,且a≠1)解的个数是( )
A.2
B.1
C.0
D.不确定的
【答案】A
【解析】解:由题意ax=﹣x2+2x+a,﹣x2+2x+a>0.
令f(x)=ax,g(x)=﹣x2+2x+a,(1)当a>1时,
f(x)=ax在(﹣∞,+∞)上单调递增,且f(0)=1,f(1)=a,
g(x)=﹣x2+2x+a在[0,1]上单调递增,在[1,+∞)上单调递减,且g(0)=a,g(1)=1+a,
在[0,1]上,f(x)<g(x),
∵g(x)在x<0及x>1时分别有一个零点,而f(x)恒大于零,
∴f(x)与g(x)的图象在x<0及x>1时分别有一个交点,
∴方程有两个解;(2)当a<1时,
f(x)=ax在(﹣∞,+∞)上单调递减,且f(0)=1,f(1)=a,
g(x)=﹣x2+2x+a在[0,1]上单调递增,在[1,+∞)上单调递减,且g(0)=a,g(1)=1+a,
f(0)>g(0),f(1)<g(1),
∴在(0,1)上f(x)与g(x)有一个交点,
又g(x)在x>1时有一个零点,而f(x)恒大于零,
∴f(x)与g(x)的图象在x>1时还有一个交点,
∴方程有两个解.
综上所述,方程有两个解.
所以答案是:A.


 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中, ![]() =
= ![]() +
+ ![]()
(Ⅰ)求△ABM与△ABC的面积之比
(Ⅱ)若N为AB中点, ![]() 与
与 ![]() 交于点P且
交于点P且 ![]() =x
=x ![]() +y
+y ![]() (x,y∈R),求x+y的值.
(x,y∈R),求x+y的值.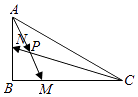
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,已知a1=2,an+1=4an﹣3n+1,n∈N .
(1)设bn=an﹣n,求证:数列{bn}是等比数列;
(2)求数列{an}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
(0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为 ![]() .
.
(Ⅰ)求 ![]() 的值;
的值;
(Ⅱ)将函数y=f(x)的图象向右平移 ![]() 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l经过直线l1:2x﹣y﹣1=0与直线l2:x+2y﹣3=0的交点P,且与直线l3:x﹣y+1=0垂直.
(1)求直线l的方程;
(2)若直线l与圆C:(x﹣a)2+y2=8相交于P,Q两点,且 ![]() ,求a的值.
,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com