
【题目】已知函数f(x)=|x﹣1|,则与y=f(x)相等的函数是( )
A.g(x)=x﹣1
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:对于A,函数g(x)=x﹣1(x∈R),与函数f(x)=|x﹣1|(x∈R)的对应关系不同,不是相等函数;
对于B,函数h(x)= ![]() =|x﹣1|(x≠1),与函数f(x)=|x﹣1|(x∈R)的定义域不同,不是相等函数;
=|x﹣1|(x≠1),与函数f(x)=|x﹣1|(x∈R)的定义域不同,不是相等函数;
对于C,函数s(x)= ![]() =x﹣1(x≥1),与函数f(x)=|x﹣1|(x∈R)的定义域不同,对应关系不同,不是相等函数;
=x﹣1(x≥1),与函数f(x)=|x﹣1|(x∈R)的定义域不同,对应关系不同,不是相等函数;
对于D,函数t(x)= ![]() =|x﹣1|(x∈R),与函数f(x)=|x﹣1|(x∈R)的定义域相同,对应关系也相同,是相等函数.
=|x﹣1|(x∈R),与函数f(x)=|x﹣1|(x∈R)的定义域相同,对应关系也相同,是相等函数.
所以答案是:D.
【考点精析】本题主要考查了判断两个函数是否为同一函数的相关知识点,需要掌握只有定义域和对应法则二者完全相同的函数才是同一函数才能正确解答此题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】定义:f1(x)=f(x),当n≥2且x∈N*时,fn(x)=f(fn﹣1(x)),对于函数f(x)定义域内的x0 , 若正在正整数n是使得fn(x0)=x0成立的最小正整数,则称n是点x0的最小正周期,x0称为f(x)的n~周期点,已知定义在[0,1]上的函数f(x)的图象如图,对于函数f(x),下列说法正确的是(写出所有正确命题的编号)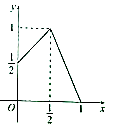
①1是f(x)的一个3~周期点;
②3是点 ![]() 的最小正周期;
的最小正周期;
③对于任意正整数n,都有fn( ![]() )=
)= ![]() ;
;
④若x0∈( ![]() ,1],则x0是f(x)的一个2~周期点.
,1],则x0是f(x)的一个2~周期点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:a∈R,且a>0,a+ ![]() ≥2,命题q:x0∈R,sinx0+cosx0=
≥2,命题q:x0∈R,sinx0+cosx0= ![]() ,则下列判断正确的是( )
,则下列判断正确的是( )
A.p是假命题
B.q是真命题
C.(¬q)是真命题
D.(¬p)∧q是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的有( ) (1.)很小的实数可以构成集合;
(2.)集合{y|y=x2﹣1}与集合{(x,y)|y=x2﹣1}是同一个集合;
(3.) ![]() 这些数组成的集合有5个元素;
这些数组成的集合有5个元素;
(4.)集合{(x,y)|xy≤0,x,y∈R}是指第二和第四象限内的点集.
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x),φ(x)满足关系φ(x)=f(x)f(x+α)(其中α是常数).
(1)如果α=1,f(x)=2x﹣1,求函数φ(x)的值域;
(2)如果α= ![]() ,f(x)=sinx,且对任意x∈R,存在x1 , x2∈R,使得φ(x1)≤φ(x)≤φ(x2)恒成立,求|x1﹣x2|的最小值;
,f(x)=sinx,且对任意x∈R,存在x1 , x2∈R,使得φ(x1)≤φ(x)≤φ(x2)恒成立,求|x1﹣x2|的最小值;
(3)如果f(x)=Asin(ωx+)(A>0,ω>0),求函数φ(x)的最小正周期(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=cos(x+ ![]() )的图象,只需把余弦曲线y=cosx上的所有的点( )
)的图象,只需把余弦曲线y=cosx上的所有的点( )
A.向左平移 ![]() 个单位长度
个单位长度
B.向右平移 ![]() 个单位长度
个单位长度
C.向左平移 ![]() 个单位长度
个单位长度
D.向右平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.若命题p为真命题,命题q为假命题,则命题“p且q”为真命题
B.“ ![]() ”是“
”是“ ![]() ”的充分不必要条件
”的充分不必要条件
C.l为直线,α,β,为两个不同的平面,若l⊥α,α⊥β,则l∥β
D.命题“?x∈R,2x>0”的否定是“?x0∈R, ![]() ≤0”
≤0”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a∈R,函数f(x)=|x2﹣2ax|,方程f(x)=ax+a的四个实数解满足x1<x2<x3<x4 .
(1)求a的取值范围;
(2)证明:f(x4)> ![]() +8
+8 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com