解:(1)∵
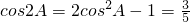
,且A为锐角
∴cosA=

,sinA=
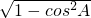
=

∵sinC=

,且C为锐角
∴cosC=
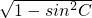
=

因此,cos(A+C)=cosAcosC-sinAsinC=

•

-

•

=

(2)∵cos(A+C)=

,0<A+C<π,∴A+C=

,得B=π-

=

,sinB=

∵sinA=

,sinB=

,sinC=

,
∴sinA:sinB:sinC=2

:5

:

由正弦定理,得a:b:c=2

:5

:

,设a=2

x,得b=5

x,c=

x
∵
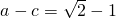
,得2

x-

x=

∴x=

,可得a=

,b=

,c=1
(3)由(2)知A+C=

,得tan(α+

)=2
∴
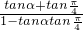
=2,解之得tanα=

所以
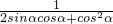
=
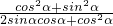
=

=

分析:(1)根据二倍角三角函数与同角三角函数的关系,算出cosA、sinA和cosC的值,最后用两角和的余弦公式,即可求出cos(A+C)的值;
(2)由(1)求出的cos(A+C)值,可得A+C=

,从而算出sinB=

,结合正弦定理得出a:b:c=2

:5

:

,再结合题意
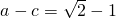
,不难得出三边a,b,c的值;
(3)由题意,tan(α+

)=2,解之得tanα=

,再将所求式的分子转化为cos
2α+sin
2α,分子分母同除以cos
2α转化为关于tanα的式子,即可得到所求式子的值.
点评:本题给出三角形的两个角A、C与边a、c的关系式,求三边的长并求三角函数式的值,着重考查了三角恒等变形、三角形内角和定理和用正余弦定理解三角形等知识,属于中档题.

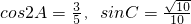 .
.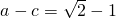 ,求a,b,c的值;
,求a,b,c的值;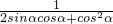 的值.
的值.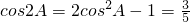 ,且A为锐角
,且A为锐角 ,sinA=
,sinA=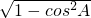 =
=
 ,且C为锐角
,且C为锐角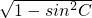 =
=
 •
• -
- •
• =
=
 ,0<A+C<π,∴A+C=
,0<A+C<π,∴A+C= ,得B=π-
,得B=π- =
= ,sinB=
,sinB=
 ,sinB=
,sinB= ,sinC=
,sinC= ,
, :5
:5 :
:
 :5
:5 :
: ,设a=2
,设a=2 x,得b=5
x,得b=5 x,c=
x,c= x
x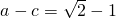 ,得2
,得2 x-
x- x=
x=
 ,可得a=
,可得a= ,b=
,b= ,c=1
,c=1 ,得tan(α+
,得tan(α+ )=2
)=2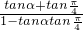 =2,解之得tanα=
=2,解之得tanα=
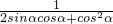 =
=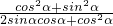 =
= =
=
 ,从而算出sinB=
,从而算出sinB= ,结合正弦定理得出a:b:c=2
,结合正弦定理得出a:b:c=2 :5
:5 :
: ,再结合题意
,再结合题意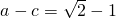 ,不难得出三边a,b,c的值;
,不难得出三边a,b,c的值; )=2,解之得tanα=
)=2,解之得tanα= ,再将所求式的分子转化为cos2α+sin2α,分子分母同除以cos2α转化为关于tanα的式子,即可得到所求式子的值.
,再将所求式的分子转化为cos2α+sin2α,分子分母同除以cos2α转化为关于tanα的式子,即可得到所求式子的值.

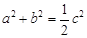 .则直线
.则直线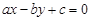 被圆
被圆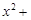
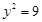 所截得的弦长为 .
所截得的弦长为 .