
如图1,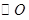 的直径AB=4,点C、D为
的直径AB=4,点C、D为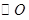 上两点,且
上两点,且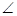 CAB=45°,
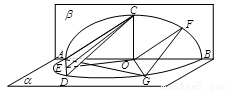
CAB=45°,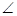 DAB=60°,F为弧BC的中点.沿直径AB折起,使两个半圆所在平面互相垂直,如图2.
DAB=60°,F为弧BC的中点.沿直径AB折起,使两个半圆所在平面互相垂直,如图2.
(I)求证:OF 平面ACD;
平面ACD;
(Ⅱ)求二面角C—AD—B的余弦值;
(Ⅲ)在弧BD上是否存在点G,使得FG 平面ACD?若存在,试指出点G的位置;若不存在,请说明理由.
平面ACD?若存在,试指出点G的位置;若不存在,请说明理由.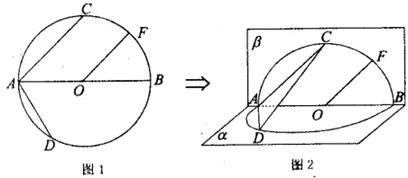
(1)对于线面平行的判定关键是证明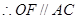 来得到。
来得到。
(2)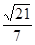
(3) 在弧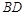 上存在点
上存在点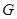 ,使得
,使得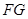 //平面
//平面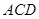 ,且点
,且点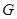 为弧
为弧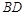 的中点
的中点
【解析】
试题分析:(方法一):证明:(Ⅰ)如右图,连接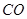 ,
,
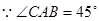 ,
, . …1分
又
. …1分
又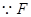 为弧
为弧 的中点,
的中点,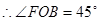 ,
,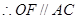 .
.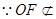 平面
平面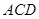 ,
, 平面
平面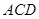 ,
,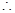
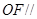 平面
平面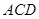 . …4分
. …4分
解:(Ⅱ)过 作
作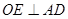 于
于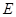 ,连
,连 .
.
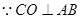 ,平面
,平面 ⊥平面
⊥平面 .
.
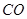 ⊥平面
⊥平面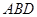 .又
.又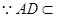 平面
平面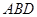 ,
, 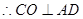 ,
, 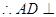 平面
平面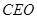 ,
,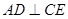 ,则∠
,则∠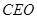 是二面角
是二面角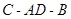 的平面角.
的平面角. 
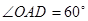 ,
,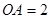 ,
, 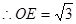 . 由
. 由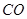 ⊥平面
⊥平面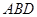 ,
,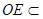 平面
平面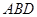 ,得
,得 为直角三角形,
为直角三角形,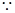
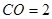 ,
,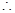
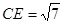
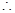
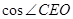 =
=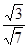 =
=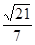 . 8分
. 8分
(Ⅲ)取弧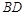 的中点
的中点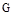 ,连结
,连结 、
、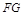 ,则
,则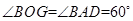
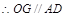 …
…
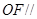 平面
平面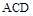 ,
, 平面
平面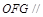 平面
平面
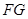 //平面
//平面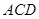 .
.
因此,在弧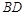 上存在点
上存在点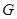 ,使得
,使得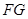 //平面
//平面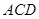 ,且点
,且点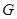 为弧
为弧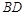 的中点.…12分
的中点.…12分
(方法二):证明:(Ⅰ)如图,以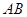 所在的直线为
所在的直线为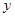 轴,以
轴,以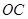 所在的直线为
所在的直线为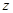 轴,以
轴,以 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系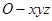
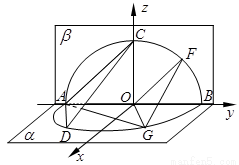
则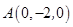
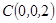 .…… 1分
.…… 1分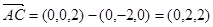 ,
,
 点
点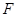 为弧
为弧 的中点,
的中点, 点
点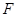 的坐标为
的坐标为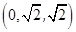 ,
,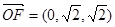 .
.
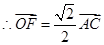 解:(Ⅱ)
解:(Ⅱ) ,
,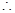 点
点 的坐标
的坐标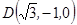 ,
,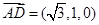 .
.
设二面角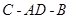 的大小为
的大小为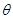 ,
,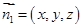 为平面
为平面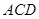 的一个法向量.
的一个法向量.
由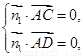 有
有 即
即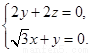
取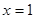 ,解得
,解得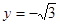 ,
,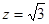 .
. 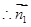 =
=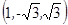 . 5分
. 5分
取平面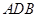 的一个法向量
的一个法向量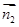 =
=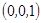 , 6分
, 6分
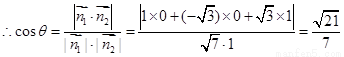 . 8分
. 8分
(Ⅲ)设在弧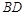 上存在点
上存在点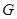
 ,
,
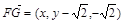 ,由(Ⅱ)知平面
,由(Ⅱ)知平面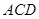 的一个法向量为
的一个法向量为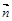 =
=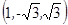 .
.
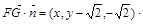
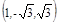 =
=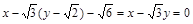 ① 9分
① 9分
又因为 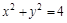 ②由①②两式联立解得
②由①②两式联立解得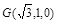 ,…11分
,…11分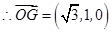 ,因为
,因为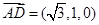 ,所以
,所以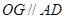 ,则
,则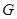 为弧
为弧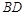 的中点,因此,在弧
的中点,因此,在弧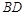 上存在点
上存在点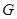 ,使得
,使得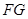 //平面
//平面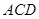 ,且点
,且点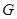 为弧
为弧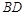 的中点. ………12分
的中点. ………12分
考点:线面平行和二面角的平面角
点评:主要是考查了二面角的求解,以及线面平行 的判定定理的运用,属于基础题。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 选做题(考生只能从A、B、C题中选作一题)
选做题(考生只能从A、B、C题中选作一题)
|
查看答案和解析>>
科目:高中数学 来源: 题型:
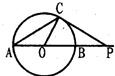
 如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,AE=AC,DE交AB于点F.
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,AE=AC,DE交AB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:
 【选做题】在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.
【选做题】在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.
|
| π |
| 4 |
| 2 |
|
| x |
| yz |
| y |
| zx |
| z |
| xy |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•盐城三模)选修4-1:几何证明选讲:
(2012•盐城三模)选修4-1:几何证明选讲: |
| AE |
 |
| AC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com