
 是一个自然数,
是一个自然数, 是
是 的各位数字的平方和,定义数列
的各位数字的平方和,定义数列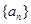 :
: 是自然数,
是自然数, (
( ,
, ).
). ,
, ;
; ,求证:
,求证: ;
; 时,求证:存在
时,求证:存在 ,使得
,使得 .
. ,
, ;(2)证明过程详见解析;(3)证明过程详见解析.
;(2)证明过程详见解析;(3)证明过程详见解析. 是a的各位数字的平方和,所以
是a的各位数字的平方和,所以 ,
, ;第二问,通过题干中给出的
;第二问,通过题干中给出的 的定义设出
的定义设出 的值,利用
的值,利用 ,得到
,得到 的值,然后用作差法比较
的值,然后用作差法比较 和
和 的大小;第三问,由已知条件
的大小;第三问,由已知条件
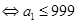 ,由于
,由于 且
且 ,得
,得 ,由归纳推理得
,由归纳推理得 ,再用数学归纳法证明一下,因此存在
,再用数学归纳法证明一下,因此存在 (
( ),有
),有 ,再分类讨论p、q的情况,得出结论.
,再分类讨论p、q的情况,得出结论. ;
; . 5分
. 5分 是一个
是一个 位数(
位数( ),
), ,
, 且
且 (
( ),且
),且 .
. 可得,
可得, .
. 所以
所以 .
. ,所以
,所以 .
. ,
, ,即
,即 . 9分
. 9分 ,即
,即 ,可知
,可知 .
. ,可知
,可知 .
. ,有
,有 .
. ,有
,有 .
. (
( ),有
),有 .
. ,
, , ,
, , ,
, ,
, ,有
,有 .
. ,即对任意
,即对任意 ,有
,有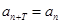 .
. ,取
,取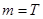 ,
, ,则有
,则有 .
. ,由
,由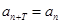 ,可得
,可得 ,
, ,
, ,则有
,则有 . 14分
. 14分

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:填空题
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.②③ | B.①②③ | C.③ | D.③④⑤ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

 ,那么
,那么 ,
, ,
, 中至少有一个不小于
中至少有一个不小于 ”时,反设正确的是( )
”时,反设正确的是( )A.假设 , , , , 至多有两个小于 至多有两个小于 |
B.假设 , , , , 至多有一个小于 至多有一个小于 |
C.假设 , , , , 都不小于 都不小于 |
D.假设 , , , , 都小于 都小于 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,
, 可被5整除,那么
可被5整除,那么 中至少有一个能被5整除”,则假设内容是_____________________________________________________.
中至少有一个能被5整除”,则假设内容是_____________________________________________________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,求证:
,求证: ,用反证法证明时,可假设
,用反证法证明时,可假设 ;
; ,
, ,求证:方程
,求证:方程 的两根的绝对值都小于1.用反证法证明时可假设方程有一根
的两根的绝对值都小于1.用反证法证明时可假设方程有一根 的绝对值大于或等于1,即假设
的绝对值大于或等于1,即假设 ,以下结论正确的是( )
,以下结论正确的是( )A. 与 与 的假设都错误 的假设都错误 |
B. 与 与 的假设都正确 的假设都正确 |
C. 的假设正确; 的假设正确; 的假设错误 的假设错误 |
D. 的假设错误; 的假设错误; 的假设正确 的假设正确 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com