
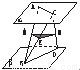
 证明:连接BC、AD,取BC的中点E,连接ME、NE,则ME是△BAC的中位线,
证明:连接BC、AD,取BC的中点E,连接ME、NE,则ME是△BAC的中位线,

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:101网校同步练习 高一数学 苏教版(新课标·2004年初审) 苏教版 题型:013
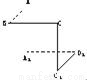
设平面α∥平面β,直线a![]() α,点b∈β,则在β内过点b的所有直线中
α,点b∈β,则在β内过点b的所有直线中
A.不一定存在与a平行的直线
B.只有两条与a平行的直线
C.存在无数条与a平行的直线
D.存在唯一一条与a平行的直线
查看答案和解析>>
科目:高中数学 来源: 题型:
A.直线a必垂直于平面β B.直线b必垂直于平面α
C.直线a不一定垂直于平面β D.过a的平面与过b的平面垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
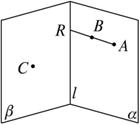
A.直线AC B.直线BC
C.直线CR D.以上均错
查看答案和解析>>
科目:高中数学 来源: 题型:
①![]()
![]() α⊥β;
α⊥β;
②![]()
![]() 平面α⊥平面ABC;
平面α⊥平面ABC;
③![]()
![]() l⊥平面ABC;
l⊥平面ABC;
④AB∥l![]() l∥平面ABC.
l∥平面ABC.
其中正确的命题是( )
A.①② B.②③ C.①③ D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com