练习册

  • 练习册
  • 试题
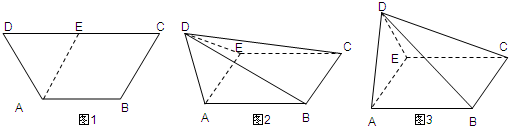    精英家教网 > 高中数学 > 题目详情
    如图1-3-2,梯形ABCD中,AD∥BC(AD＜BC),E为AD的中点,连结CE并延长交BA的延长线于G,交BD于F.求证:EF·CG=EG·CF.

    图1-3-2

    证明:∵AE∥BC,∴△AEG∽△BCG.∴.

    又∵ED∥BC,

    ∴△DEF∽△BCF.∴=.

    ∵E为AD的中点,∴=.∴=.

    ∴EFCG=EGCF.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图1，等腰梯形ABCD中，AB=2，CD=4，∠ADC=∠BCD=60°．取线段CD中点E，将△ADE沿AE折起，如图2所示．
    （1）当平面ADE折到与底面ABCE所成的二面角为900时，如图3所示，求此时二面角A-BD-C平面角的余弦值．
    （2）在将△ADE开始折起到与△ABE重合的过程中，求直线DC与平面ABCE所成角的正切值的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图1，等腰梯形ABCD中，AD∥BC，AB=AD，∠ABC=60°，E是BC的中点．将△ABE沿AE折起后如图2，使二面角B-AE-C成直二面角，设F是CD的中点，P是棱BC的中点．
    （1）求证：AE⊥BD；
    （2）求证：平面PEF⊥平面AECD；
    （3）判断DE能否垂直于平面ABC，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （09年湖南师大附中月考理）(12分)

    如图(1)在直角梯形中，∥，，

    ，，、、分别是

    线段、、的中点，现将折起，使平面

    平面 (如图(2))。

    (1)求证：∥平面；

    (2)求二面角的大小；

    (3)在线段上确定一点，使平面，请给出证明。

     

     

     

     

     

     

     

    查看答案和解析>>

    科目：高中数学 来源：江西省重点中学盟校2010届高三第二次联考理科试题 题型：解答题

    （本小题满分12分）
    将如图1的直角梯形ABEF（图中数字表示对应线段的长度）沿直线CD折成直二面角，连结EB、FB、FA后围成一个空间几何体如图2所示，
    （1）求异面直线BD与EF所成角的大小；
    （2）求二面角D—BF—E的大小；
    （3）求这个几何体的体积.

    查看答案和解析>>

    同步练习册答案