
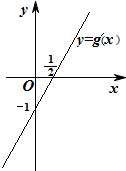
| 1 |
| 2 |
| 1 |
| x |
| 1-x |
| x |
2(x-
| ||
| 2x2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x | (0,x0) | x0 | (x0,1) | 1 | (1,+∞) |
| h'(x) | - | 0 | + | 0 | - |
| h(x) | ↘ | 极小值 | ↗ | 极大值1 | ↘ |
| x | 20 |
| x | 20 |
| x | 20 |
| 1 |
| 2 |
| 3 |
| 4 |


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:
| y1-y2 | x1-x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:044
已知函数f(x)=x2-1(x≥1)的图象为 C1,曲线C2与C1关于直线y=x对称。
(1)求曲线C2的方程y=g(x);
(2)设函数y=g(x)的定义域为M,xl,x2∈ M,且xl≠x2,求证|g(x1)-g(x2)|<|x1-x2|;
(3)设A,B为曲线C2上任意不同两点,证明直线AB与直线y=x必相交。
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
(1)求曲线C2的方程y=g(x);
(2)设函数y=g(x)的定义域为M,xl,x2∈ M,且xl≠x2,求证|g(x1)-g(x2)|<|x1-x2|;
(3)设A,B为曲线C2上任意不同两点,证明直线AB与直线y=x必相交。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省深圳市高三第一次调研考试理科数学试卷(解析版) 题型:选择题
函数y=f(x),x∈D,若存在常数C,对任意的xl∈D,仔在唯一的x2∈D,使得 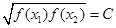 ,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为
,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为
A.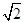 B.2 C.4
D. 2
B.2 C.4
D. 2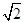
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省淮北市高三第一次模拟考试文科数学 题型:解答题
.(本题满分13分)设函数 ,方程f(x)=x有唯一的解,
,方程f(x)=x有唯一的解,
已知f(xn)=xn+1(n∈N﹡)且f(xl)= .
.
(1)求证:数列{ )是等差数列;
)是等差数列;
(2)若 ,求Sn=b1+b2+b3+…+bn
,求Sn=b1+b2+b3+…+bn
(3)在(2)的条件下,是否存在最小正整数m,使得对任意n∈N﹡,有 成立,若存在,求出m的值;若不存在,请说明理由。
成立,若存在,求出m的值;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com