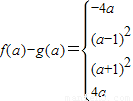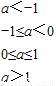已知函数y=x2-2ax+1在[-1，1]上的最大值为f（a），最小值为g（a）．
（1）求f（a）-g（a）的解析式；
（2）求f（a）-g（a）的最大值，最小值．
【答案】
分析：（1）先确定函数的对称轴和开口方向，由于函数既要求最大值，又要求最小值，需分四种情形讨论，最后将最大值与最小值做差即可得函数f（a）-g（a）
（2）先画出函数f（a）-g（a）的图象，再数形结合求出f（a）-g（a）的最值即可
解答：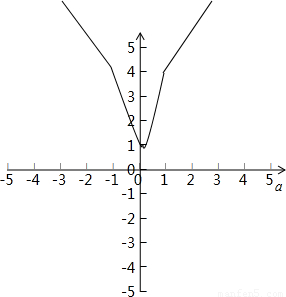
解：（1）函数y=x
2-2ax+1的对称轴为x=a，开口向上，
∴当a＜-1时，函数在[-1，1]上为增函数，最大值为2-2a，最小值为2+2a
当-1≤a＜0时，函数在[-1，a]上为减函数，在[a，1]上为增函数，最大值为2-2a，最小值为1-a
2
当0≤a≤1时，函数在[-1，a]上为减函数，在[a，1]上为增函数，最大值为2+2a，最小值为1-a
2当a＞1时，函数在[-1，1]上为减函数，最大值为2+2a，最小值为2-2a
∴
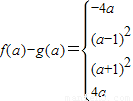
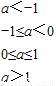
（2）函数f（a）-g（a）的图象如图，
∴所求函数有最小值1，无最大值
点评：本题考查了二次函数的图象和性质，特别是求二次函数的最值，需要分类讨论，做到不重不漏，解题时要学会用数形结合的思想方法解决问题
