
若无穷数列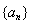 满足:①对任意
满足:①对任意 ,
, ;②存在常数
;②存在常数 ,对任意
,对任意 ,
, ,则称数列
,则称数列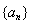 为“
为“ 数列”.
数列”.
(Ⅰ)若数列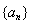 的通项为
的通项为
 ,证明:数列
,证明:数列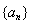 为“
为“ 数列”;
数列”;
(Ⅱ)若数列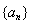 的各项均为正整数,且数列
的各项均为正整数,且数列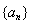 为“
为“ 数列”,证明:对任意
数列”,证明:对任意 ,
, ;
;
(Ⅲ)若数列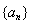 的各项均为正整数,且数列
的各项均为正整数,且数列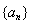 为“
为“ 数列”,证明:存在
数列”,证明:存在 ,数列
,数列 为等差数列.
为等差数列.
(Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)详见解析
【解析】
试题分析:(Ⅰ)用作差法证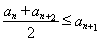 ,用单调性证
,用单调性证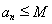 。(Ⅱ)用反证法证明。即假设存在正整数
。(Ⅱ)用反证法证明。即假设存在正整数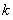 ,使得
,使得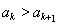 。根据
。根据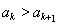 和
和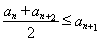 结合放缩法推倒论证得出与已知各项均为正整数相矛盾,则说明假设不成立即原命题成立。(Ⅲ)由(Ⅱ)知
结合放缩法推倒论证得出与已知各项均为正整数相矛盾,则说明假设不成立即原命题成立。(Ⅲ)由(Ⅱ)知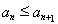 ,需分
,需分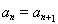 和
和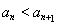 两种情况讨论,结合已知
两种情况讨论,结合已知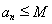 推理论证,根据等差的定义可证得存在
推理论证,根据等差的定义可证得存在 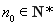 ,数列
,数列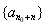 为等差数列.本题的关键是当
为等差数列.本题的关键是当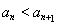 可变形得
可变形得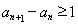 ,再用累加法表示
,再用累加法表示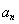 ,即
,即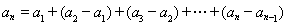 ,根据
,根据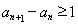 进行推理论证。
进行推理论证。
试题解析:(Ⅰ)证明:由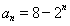 ,可得
,可得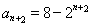 ,
,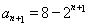 ,
,
所以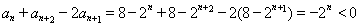 ,
,
所以对任意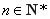 ,
,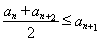 .
.
又数列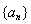 为递减数列,所以对任意
为递减数列,所以对任意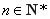 ,
,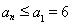 .
.
所以数列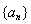 为“
为“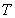 数列”. 5分
数列”. 5分
(Ⅱ)证明:假设存在正整数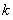 ,使得
,使得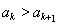 .
.
由数列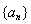 的各项均为正整数,可得
的各项均为正整数,可得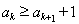 .
.
由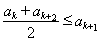 ,可得
,可得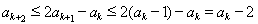 .
.
且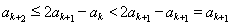 .
.
同理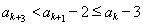 ,
,
依此类推,可得,对任意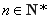 ,有
,有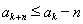 .
.
因为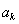 为正整数,设
为正整数,设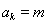 ,则
,则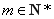 .
.
在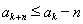 中,设
中,设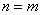 ,则
,则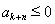 .
.
与数列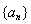 的各项均为正整数矛盾.
的各项均为正整数矛盾.
所以,对任意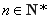 ,
,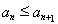 . 10分
. 10分
(Ⅲ)因为数列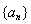 为“
为“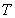 数列”,
数列”,
所以,存在常数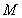 ,对任意
,对任意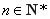 ,
,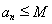 .
.
设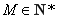 .
.
由(Ⅱ)可知,对任意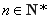 ,
,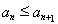 ,
,
则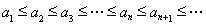 .
.
若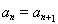 ,则
,则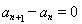 ;若
;若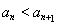 ,则
,则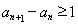 .
.
而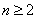 时,有
时,有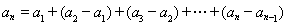 .
.
所以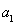 ,
,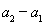 ,
,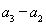 ,
,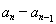 ,中最多有
,中最多有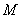 个大于或等于
个大于或等于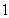 ,
,
否则与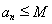 矛盾.
矛盾.
所以,存在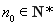 ,对任意的
,对任意的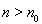 ,有
,有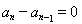 .
.
所以,对任意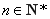 ,
,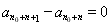 .
.
所以,存在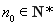 ,数列
,数列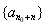 为等差数列. 14分
为等差数列. 14分
考点:新概念问题。


科目:高中数学 来源:数学教研室 题型:044
①输入数据![]() ∈D,经数列发生器输出
∈D,经数列发生器输出![]() =f(
=f(![]() );
);
②若![]()
![]() D,则数列发生器结束工作;若
D,则数列发生器结束工作;若![]() ∈D则将
∈D则将![]() 反馈回输入端,再输出
反馈回输入端,再输出![]() =f(
=f(![]() ),并依此规律继续下去,现定义
),并依此规律继续下去,现定义![]() .
.
(1)若输入![]() ,则由数列发生器发生数列{
,则由数列发生器发生数列{![]() },请写出数列{
},请写出数列{![]() }的所有项;
}的所有项;
(2)若要数列发生器产生一个无穷数列的常数,试求输入的初始数据![]() 的值;
的值;
(3)若输入![]() 时,产生的无穷数列{
时,产生的无穷数列{![]() }满足:对任意正整数n,均有
}满足:对任意正整数n,均有![]() 求
求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:044
对任意函数f(x).x∈D.可按下图所示构造一个数列发生器,其工作原理如下:
①输入数据![]() ∈D,经数列发生器输出
∈D,经数列发生器输出![]() =f(
=f(![]() );
);
②若![]()
![]() D,则数列发生器结束工作;若
D,则数列发生器结束工作;若![]() ∈D则将
∈D则将![]() 反馈回输入端,再输出
反馈回输入端,再输出![]() =f(
=f(![]() ),并依此规律继续下去,现定义
),并依此规律继续下去,现定义![]() .
.
(1)若输入![]() ,则由数列发生器发生数列{
,则由数列发生器发生数列{![]() },请写出数列{
},请写出数列{![]() }的所有项;
}的所有项;
(2)若要数列发生器产生一个无穷数列的常数,试求输入的初始数据![]() 的值;
的值;
(3)若输入![]() 时,产生的无穷数列{
时,产生的无穷数列{![]() }满足:对任意正整数n,均有
}满足:对任意正整数n,均有![]() 求
求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
![]()
![]() ,构造一个数列发生器,其工作原理如下:
,构造一个数列发生器,其工作原理如下:
输入数据![]() ,经数列发生器输出
,经数列发生器输出![]() ,若
,若![]() ,则数列发生器结束工作,
,则数列发生器结束工作,
若![]() ,则将
,则将![]() 反馈回输入端,再输出
反馈回输入端,再输出![]() 并依此规律继续下去,若输入
并依此规律继续下去,若输入![]() 时,产生的无穷数列
时,产生的无穷数列![]() 满足,对任意正整数
满足,对任意正整数![]() 均有
均有![]() ,求
,求![]() 范围
范围
查看答案和解析>>
科目:高中数学 来源: 题型:
对任意函数![]() ,
,![]() ,可按图示构造一个数列发生器,其工作原理如下:①输入数据
,可按图示构造一个数列发生器,其工作原理如下:①输入数据![]() ,经数列发生器输出
,经数列发生器输出![]() ;②若
;②若![]() ,则数列发生器结束工作;若
,则数列发生器结束工作;若![]() ,则将
,则将![]() 反馈回输入端,再输出
反馈回输入端,再输出![]() ,并依此规律继续下去。现定义
,并依此规律继续下去。现定义![]() 。
。
 (1)若输入
(1)若输入![]() ,则由数列发生器产生数列
,则由数列发生器产生数列![]() ,请写出数列
,请写出数列![]() 的所有项;
的所有项;
(2)若要数列发生器产生一个无穷的常数数列,试求输入的初始数据![]() 的值;
的值;
(3)若输入![]() 时,产生的无穷数列
时,产生的无穷数列![]() 满足:对任意正整数
满足:对任意正整数![]() ,均有
,均有![]() ,求
,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com