Question

已知函数f（x）=（x²+ax-2a²+3a）e^x（x∈R），若a∈R，求函数f（x）的单调区间与极值．

Answer 1

分析：求出函数的导数，对a进行讨论，分别判断函数的单调性，最后根据a的不同取值得出的结论综上所述即可

解答：解：f′（x）=[x²+（a+2）x-2a²+4a]e^x
令f′（x）=0  解得x=-2a  或x=a-2以下分三种情况讨论．
（1）若a＞

2

3

，则-2a＜a-2．当x变化时，f′（x），f（x）的变化如下表：
-
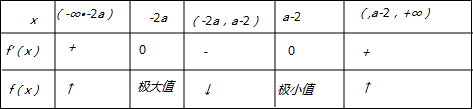
所以f（x）在（-∞，-2a），（a-2，+∞）内是增函数在（-a，a-2）内是减函数
函数f（x）在x=2处取得极大值f（-2a），且f（-2a）=3ae^-2a
函数f（x）在x=a-2处取得极小值f（a-2），且f（a-2）=（4-3a）e^a-2
（2）若a＜

2

3

则-2a＞a-2
当x变化时，f′（x），f（x）的变化如下表：

函数f（x）在x=2处取得极小值f（-2a），且f（-2a）=3ae^-2a
函数f（x）在x=a-2处取得极大值f（a-2），且f（a-2）=（4-3a）e^a-2
（3）若a=

2

3

则-2a=a-2函数f（x）在（-∞，+∞）内单调递增，此时函数无极值

点评：考查函数导数的求导，做题时要注意对a进行讨论，最后得出函数的极值和单调区间