

| A. | 3955 | B. | 3957 | C. | 3959 | D. | 3961 |
分析 观察乙图,发现第k行有k个数,第k行最后的一个数为k2,前k行共有$\frac{k(k+1)}{2}$个数,然后以判断出这个2012个数在第63行,第59个数,求出第63行第一个数,而第63行相邻两个数相差2,得到第63行58个数值,即可求出所求.
解答 解:图乙中第k行有k个数,第k行最后的一个数为k2,前k行共有$\frac{k(k+1)}{2}$个数,
前62行有1953个数,由2012个数出现在第63行,第59个数,
第62行第一个数为622+1=3845,公差为2的等差数列
∴a2010=3845+(59-1)×2=3961,
故选:D.
点评 本题主要考查学生会根据图形归纳总结规律来解决问题,会进行数列的递推式运算,同时考查计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥底面ABCD,E、F分别为AB、PC的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥底面ABCD,E、F分别为AB、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
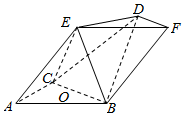 如图,多面体ABCDEF中,四边形ABEF是平行四边形,DF∥BC,BC=BF=2DF=2$\sqrt{2}$,∠BAC=90°,AB=AC,点E在底面ABC的射影为BC的中点O.
如图,多面体ABCDEF中,四边形ABEF是平行四边形,DF∥BC,BC=BF=2DF=2$\sqrt{2}$,∠BAC=90°,AB=AC,点E在底面ABC的射影为BC的中点O.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$ | B. | 0 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com