
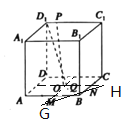
【题目】在正方体![]() 中边长AB为2,P为正方形A1B1C1D1四边上的动点,O为底面正方形ABCD的中心,Q为正方形ABCD内一点,M,N分别为AB,BC上靠近A和C的三等分点,若线段
中边长AB为2,P为正方形A1B1C1D1四边上的动点,O为底面正方形ABCD的中心,Q为正方形ABCD内一点,M,N分别为AB,BC上靠近A和C的三等分点,若线段![]() 与OP相交且互相平分,则点Q的轨迹与线段MN形成的封闭图形的面积为____.
与OP相交且互相平分,则点Q的轨迹与线段MN形成的封闭图形的面积为____.

【答案】![]()
【解析】
根据线段![]() 与OP互相平分,可得四边形
与OP互相平分,可得四边形![]() 是平行四边形,点Q的轨迹为过O与AB,AD平行的两条线段,设过O平行于AB的直线交MN于点H,过O平行于AD的直线与MN交于点G,则点Q的轨迹与线段MN形成的封闭图形是等腰直角△GHO,由此能求出点Q的轨迹与线段MN形成的封闭图形的面积.
是平行四边形,点Q的轨迹为过O与AB,AD平行的两条线段,设过O平行于AB的直线交MN于点H,过O平行于AD的直线与MN交于点G,则点Q的轨迹与线段MN形成的封闭图形是等腰直角△GHO,由此能求出点Q的轨迹与线段MN形成的封闭图形的面积.
解:∵线段![]() 与OP互相平分,
与OP互相平分,
∴四边形![]() 是平行四边形
是平行四边形
∴![]() ∥
∥![]()
∵O为底面正方形ABCD的中心,
∴点Q的轨迹为两条线段(过O与AB,AD平行的两条线段),
设过O平行于AB的直线交MN于点H,过O平行于AD的直线与MN交于点G,
∴点Q的轨迹与线段MN形成的封闭图形是等腰直角△GHO,
∵![]() ,
,![]()
∴点Q的轨迹与线段MN形成的封闭图形的面积为:![]()
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+1+|3-x|,x≥-1.
(1)求不等式f(x)≤6的解集;
(2)若f(x)的最小值为n,正数a,b满足2nab=a+2b,求2a+b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中有如下间题:“今有甲、乙、丙、丁、戊五人分五饯,令上二人所得与下三人等,且五人所得钱按顺序等次差,问各得几何?”其意思为“甲、乙、丙、丁、戊五人分五钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列,问五人各得多少钱(钱:古代一种重量单位)?”这个问题中丙所得为( )
A. ![]() 钱 B.
钱 B. ![]() 钱 C. 1钱 D.
钱 C. 1钱 D. ![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的公差
的公差![]() 大于0,且
大于0,且![]() ,
,![]() 是方程
是方程![]() 的两根,数列
的两根,数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,试比较
,试比较![]() 与
与![]() 的大小,并用数学归纳法给予证明.
的大小,并用数学归纳法给予证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长度为![]() 的线段
的线段![]() 的两个端点
的两个端点![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴上运动,动点
轴上运动,动点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 且斜率不为零的直线
且斜率不为零的直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() 、
、![]() ,在
,在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 的斜率之积为常数.若存在,求出定点
的斜率之积为常数.若存在,求出定点![]() 的坐标以及此常数;若不存在,请说明理由.
的坐标以及此常数;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.

(1)如图,设直线![]() 将坐标平面分成
将坐标平面分成![]() 四个区域(不含边界),若函数
四个区域(不含边界),若函数![]() 的图象恰好位于其中一个区域内,判断其所在的区域并求对应的
的图象恰好位于其中一个区域内,判断其所在的区域并求对应的![]() 的取值范围;
的取值范围;
(2)当![]() 时,求证:
时,求证:![]() 且
且![]() ,有
,有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解校园噪音情况,学校环保协会对校园噪音值(单位:分贝)进行了![]() 天的监测,得到如下统计表:
天的监测,得到如下统计表:
噪音值(单位:分贝) |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)根据该统计表,求这![]() 天校园噪音值的样本平均数(同一组的数据用该组组间的中点值作代表).
天校园噪音值的样本平均数(同一组的数据用该组组间的中点值作代表).
(2)根据国家声环境质量标准:“环境噪音值超过![]() 分贝,视为重度噪音污染;环境噪音值不超过
分贝,视为重度噪音污染;环境噪音值不超过![]() 分贝,视为度噪音污染.”如果把由上述统计表算得的频率视作概率,回答下列问题:
分贝,视为度噪音污染.”如果把由上述统计表算得的频率视作概率,回答下列问题:
(i)求周一到周五的五天中恰有两天校园出现重度噪音污染而其余三天都是轻度噪音污染的概率.
(ii)学校要举行为期![]() 天的“汉字听写大赛”校园选拔赛,把这
天的“汉字听写大赛”校园选拔赛,把这![]() 天校园出现的重度噪音污染天数记为
天校园出现的重度噪音污染天数记为![]() ,求
,求![]() 的分布列和方差
的分布列和方差![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com