
根据我国汽车制造的现实情况,一般卡车高3 m,宽1.6 m.现要设计横断面为抛物线型的双向二车道的公路隧道,为保障双向行驶安全,交通管理规定汽车进入隧道后必须保持距中线0.4 m的距离行驶.已知拱口AB宽恰好是拱高OC的4倍,若拱宽为a m,求能使卡车安全通过的a的最小整数值.
14m
【解析】
试题分析:根据问题的实际意义,卡车通过隧道时应以卡车沿着距隧道中线0.4m到2m间的道路行驶为最佳路线,因此,卡车能否安全通过,取决于距隧道中线2m(即在横断面上距拱口中点2m)处隧道的高度是否够3m,据此可通过建立坐标系,确定出抛物线的方程后求得.
【解析】
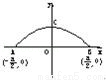
如图,以拱口AB所在直线为x轴,以拱高OC所在直线为y轴建立直角坐标系,由题意可得抛物线的方程为x2=﹣2p(y﹣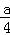 ),
),
∵点A(﹣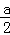 ,0)在抛物线上,
,0)在抛物线上,
∴(﹣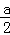 )2=﹣2p(0﹣
)2=﹣2p(0﹣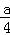 ),得p=
),得p=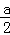 .
.
∴抛物线方程为x2=﹣a(y﹣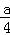 ).
).
取x=1.6+0.4=2,代入抛物线方程,得
22=﹣a(y﹣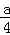 ),y=
),y=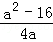 .
.
由题意,令y>3,得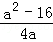 >3,
>3,
∵a>0,∴a2﹣12a﹣16>0.
∴a>6+2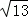 .
.
又∵a∈Z,∴a应取14,15,16,.
答:满足本题条件使卡车安全通过的a的最小正整数为14m.


科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.4 生活中的优化问题举例练习卷(解析版) 题型:解答题
一艘轮船在航行中的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问此轮船以何种速度航行时,能使行驶每公里的费用总和最小?
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.4 圆锥曲线的应用练习卷(解析版) 题型:解答题
(2003•上海)如图,某隧道设计为双向四车道,车道总宽22米,要求通行车辆限高4.5米,隧道全长2.5千米,隧道的拱线近似地看成半个椭圆形状.
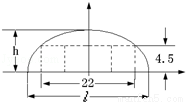
(1)若最大拱高h为6米,则隧道设计的拱宽l是多少?
(2)若最大拱高h不小于6米,则应如何设计拱高h和拱宽l,才能使半个椭圆形隧道的土方工程量最最小?(半个椭圆的面积公式为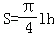 ,柱体体积为:底面积乘以高.本题结果精确到0.1米)
,柱体体积为:底面积乘以高.本题结果精确到0.1米)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.4 圆锥曲线的应用练习卷(解析版) 题型:填空题
(5分)在相距1400 m的A、B两哨所,听到炮弹爆炸声音的时间相差3 s,已知声速340 m/s.炮弹爆炸点所在曲线的方程为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.3 抛物线练习卷(解析版) 题型:解答题
设F(1,0),点M在x轴上,点P在y轴上,且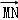 =2
=2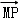 ,
,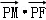 =0;
=0;
(1)当点P在y轴上运动时,求点N的轨迹C的方程;
(2)设A(x1,y1),B(x2,y2),D(x3,y3)是曲线C上除去原点外的不同三点,且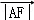 ,
,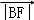 ,
, 成等差数列,当线段AD的垂直平分线与x轴交于点E(3,0)时,求点B的坐标.
成等差数列,当线段AD的垂直平分线与x轴交于点E(3,0)时,求点B的坐标.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.1 椭圆练习卷(解析版) 题型:选择题
(3分)已知椭圆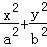 =1(a>b>0)的离心率是
=1(a>b>0)的离心率是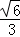 ,过椭圆上一点M作直线MA,MB分别交椭圆于A,B两点,且斜率分别为k1,k2,若点A,B关于原点对称,则k1•k2的值为( )
,过椭圆上一点M作直线MA,MB分别交椭圆于A,B两点,且斜率分别为k1,k2,若点A,B关于原点对称,则k1•k2的值为( )
A. B.﹣
B.﹣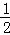 C.
C. D.﹣
D.﹣
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版必修二 3.1 弧度制与任意角练习卷2(解析版) 题型:选择题
(2分)在半径为10cm的圆中,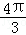 的圆心角所对弧长为( )
的圆心角所对弧长为( )
A. π B.
π B.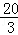 π C.
π C.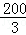 π D.
π D.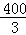 π
π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com