
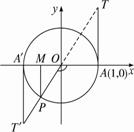
图1-2-1
A.正弦线MP,正切线A′T′
B.正弦线PM,正切线AT
C.正弦线MP,正切线AT
D.正弦线PM,正切线A′T′
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
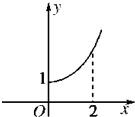 定义在R上的偶函数f(x)的部分图象如图所示,则在(-2,0)上,下列函数中与f(x)的单调性不同的是( )
定义在R上的偶函数f(x)的部分图象如图所示,则在(-2,0)上,下列函数中与f(x)的单调性不同的是( )| A、y=x2+1 | |||||
| B、y=|x|+1 | |||||
C、y=
| |||||
D、y=
|
查看答案和解析>>
科目:高中数学 来源: 题型:
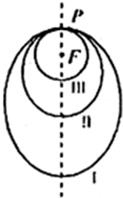 给出下列5个命题:
给出下列5个命题:| 1 |
| 5 |
| 1 |
| 1-a |
| 2a |
tan2x+
| ||
|
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
定义在R上的偶函数f(x)的部分图象如图所示,则在(-2,0)上,下列函数中与f(x)的单调性不同的是( )
A.y=x2+1
B.y=|x|+1
C.y=
D.y=
查看答案和解析>>
科目:高中数学 来源:2011年广东省高考数学一轮课时训练:2.3 平面向量的基本定理及坐标表示(新人教必修4)(解析版) 题型:解答题
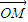 =x
=x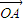 ,
,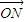 =y
=y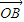
 +x,判断F(x)的单调性,并给出你的证明.
+x,判断F(x)的单调性,并给出你的证明.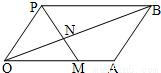
查看答案和解析>>
科目:高中数学 来源:2011年四川省自贡市高考数学三模试卷(理科)(解析版) 题型:解答题
 是函数f(x)=ax2+2(a-1)x+2在区间(-∞,4]上为单调减函数的充要条件;
是函数f(x)=ax2+2(a-1)x+2在区间(-∞,4]上为单调减函数的充要条件; >1+a>
>1+a> ;
; (x≠kπ+
(x≠kπ+ ),k∈Z,/为虚数单位)的最小值为2;
),k∈Z,/为虚数单位)的最小值为2;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com