练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    化简（ ）

    A．1 B． C． D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    16．如图，在四棱锥P-ABCD中，侧面PAD是正三角形，底面ABCD直角梯形，AD∥BC，∠ADC=90°，AD=2BC=2，$CD=\sqrt{3}$，平面PAD⊥底面ABCD，若M为AD的中点．
    （Ⅰ）求证：BM⊥面PAD；
    （Ⅱ）在线段PC上是否存在点E，使二面角E-BM-C等于30°，若存在，求$\frac{PE}{EC}$的值，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．等差数列{an}的公差为d，前n项和Sn，设n≥3m，m∈N+，判断A=Sm，B=S2m-Sm，C=S3m-S2m三者是否也成等差数列？若成等差数列，求其公差．

    查看答案和解析>>

    科目：高中数学 来源：2017届四川成都七中高三10月段测数学（理）试卷（解析版） 题型：解答题

    调查表明，高三学生的幸福感与成绩，作业量，人际关系的满意度的指标有极强的相关性，现将这三项的满意度指标分别记为，并对它们进行量化：0表示不满意，1表示基本满意，2表示满意．再用综合指标的值评定高三学生的幸福感等级：若，则幸福感为一级；若，则幸福感为二级；若，则幸福感为三级. 为了了解目前某高三学生群体的幸福感情况，研究人员随机采访了该群体的10名高三学生，得到如下结果：

    （1）在这10名被采访者中任取两人，求这两人的成绩满意度指标相同的概率；

    （2）从幸福感等级是一级的被采访者中任取一人，其综合指标为，从幸福感等级不是一级的被采访者中任取一人，其综合指标为，记随机变量，求的分布列及其数学期望.

    查看答案和解析>>

    科目：高中数学 来源：2017届四川成都七中高三10月段测数学（理）试卷（解析版） 题型：选择题

    定义域为的连续可导函数，若满足以下两个条件：

    ①的导函数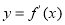没有零点，

    ②对，都有.

    则关于方程有（ ）个解.

    A．2 B．1 C．0 D．以上答案均不正确

    查看答案和解析>>

    科目：高中数学 来源：2017届四川成都七中高三10月段测数学（理）试卷（解析版） 题型：选择题

    已知，则复数（ ）

    A． B． C． D．

    查看答案和解析>>

    科目：高中数学 来源：2017届山东潍坊临朐县高三10月月考数学（文）试卷（解析版） 题型：解答题

    已知命题指数函数单调递增；命题，.若命题“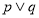”为真命题，命题“”为假命题，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源：2017届江西省红色七校高三上学期联考一数学（文）试卷（解析版） 题型：解答题

    如图，椭圆：（）的短轴长为，点在C上，平行于OM的直线交椭圆C于不同的两点A，B．

    （1）求椭圆的方程；

    （2）证明：直线MA，MB与轴总围成等腰三角形．

    查看答案和解析>>

    科目：高中数学 来源：2017届河北正定中学高三上月考一数学（理）试卷（解析版） 题型：解答题

    选修4-4：坐标系与参数方程

    在直角坐标系中，以坐标原点为极点，轴的非负半轴为极轴建立极坐标系．已知点的极坐标为，曲线 的参数方程为（为参数）．

    （1）直线过且与曲线相切，求直线的极坐标方程；

    （2）点与点关于轴对称，求曲线上的点到点的距离的取值范围．

    查看答案和解析>>

    同步练习册答案