
已知三次函数![]() 在
在![]() 和
和![]() 时取极值,且
时取极值,且![]() .(Ⅰ) 求函数
.(Ⅰ) 求函数![]() 的表达式;(Ⅱ)求函数
的表达式;(Ⅱ)求函数![]() 的单调区间和极值;(Ⅲ)若函数
的单调区间和极值;(Ⅲ)若函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,试求
,试求![]() 、应满足的条件。
、应满足的条件。
解:(Ⅰ)![]() ,
,
由题意得:![]() 是
是![]() 的两个根,
的两个根,
解得,![]() .
.
再由![]() 可得
可得![]() . -----------------2分
. -----------------2分
∴![]() . ------------------4分
. ------------------4分
(Ⅱ) 解:![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;------------------5分
;------------------5分
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;------------------6分
;------------------6分
当![]() 时,
时,![]() .∴函数
.∴函数![]() 在区间
在区间![]() 上是增函数; ------------------7分
上是增函数; ------------------7分
在区间![]() 上是减函数;在区间
上是减函数;在区间![]() 上是增函数.
上是增函数.
函数![]() 的极大值是
的极大值是![]() ,极小值是
,极小值是![]() . ------------------9分
. ------------------9分
(Ⅲ) 解:函数![]() 的图象是由
的图象是由![]() 的图象向右平移
的图象向右平移![]() 个单位,向上平移4
个单位,向上平移4![]() 个单位得到,
个单位得到,
所以,函数![]() 在区间
在区间![]() 上的值域为
上的值域为
![]() (
(![]() ). -------------10分
). -------------10分
而![]() ,∴
,∴![]() ,
,
即![]() .
.
则函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() .------------------12分
.------------------12分
令![]() 得
得![]() 或
或![]() .
.
由![]() 的单调性知,
的单调性知,![]() ,即
,即![]() .
.
综上所述,![]() 、应满足的条件是:
、应满足的条件是:![]() ,且
,且![]() ------------------14分
------------------14分


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省高三3月月考文科数学试卷 题型:解答题
已知三次函数 在
在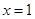 和
和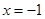 时取极值,且
时取极值,且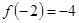 。
。 求函数
求函数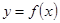 的表达式;
的表达式; 求函数
求函数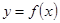 的单调区间和极值;
的单调区间和极值; 若函数
若函数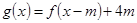
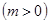 在区间
在区间 ,
, 上的值域为
上的值域为 ,16
,16 ,试求
,试求 、
、 应满足的条件。
应满足的条件。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com