
分析 (1)代入,求导,利用导数的概念求值即可;
(2)对不等式整理得m>$\frac{x+1}{{e}^{x}}$,构造函数,利用导函数求出右式的最大值即可.
(3)把零点代入,对函数整理为y=(e${\;}^{{x}_{2}}$-e${\;}^{{x}_{1}}$)($\frac{1}{{e}^{{x}_{2}}+{e}^{{x}_{1}}}$-m)=$\frac{{e}^{{x}_{2}-{x}_{1}}-1}{{e}^{{x}_{2}-{x}_{1}}+1}$-(x2-x1),利用换元法令x2-x1=t,得出函数g(t)=$\frac{{e}^{t}-1}{{e}^{t}+1}$-t(t>0),利用导函数得出函数的单调性,根据单调性得出函数的值域.
解答 解:(1)当x=0时,f(0)=m-1=1,
∴m=2,
∵f'(x)=2ex-1,f'(0)=1,
∴所求切线方程y=x+1,即x-y+1=0;
(2)由f(x)>0得mex-x-1>0,即有m>$\frac{x+1}{{e}^{x}}$
令μ(x)=$\frac{x+1}{{e}^{x}}$,则μ'(x)=$\frac{-x}{{e}^{x}}$,…(5分)
令μ'(x)=$\frac{-x}{{e}^{x}}$>0得x<0,μ'(x)=$\frac{-x}{{e}^{x}}$<0得x>0
∴μ(x)在(-∞0)上单调递增,在(0,+∞)上单调递减.
∴μ(x)的最大值为μ(0)=1,
∴m>1;
(3)由题意,mex1-x1-1=0,mex2-x2-1=0. …(9分)
y=(e${\;}^{{x}_{2}}$-e${\;}^{{x}_{1}}$)($\frac{1}{{e}^{{x}_{2}}+{e}^{{x}_{1}}}$-m)=$\frac{{e}^{{x}_{2}-{x}_{1}}-1}{{e}^{{x}_{2}-{x}_{1}}+1}$-(x2-x1)
令x2-x1=t
g(t)=$\frac{{e}^{t}-1}{{e}^{t}+1}$-t(t>0),
∵g'(t)=$\frac{-{e}^{2t}-1}{({e}^{t}+1)^{2}}$<0,
∴g(t)在(0,+∞)在上单调递减,
∴g(t)<g(0)=0.
∴g(t)∈(-∞,0)
∴y=(e${\;}^{{x}_{2}}$-e${\;}^{{x}_{1}}$)($\frac{1}{{e}^{{x}_{2}}+{e}^{{x}_{1}}}$-m)的值域为(-∞,0).
点评 本题考查了导函数的应用,函数的构造,换元法的应用和零点的概念.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:选择题
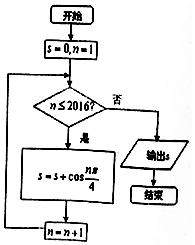
| A. | 0 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$+1 | D. | $\sqrt{2}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {1,2,3} | C. | {0,1,2} | D. | {1,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
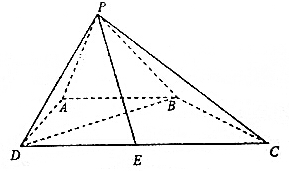 如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD都是边长为1的正三角形,DC=2,E为DC的中点.
如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD都是边长为1的正三角形,DC=2,E为DC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 5 | 25 | 30 | 25 | 15 |
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 10 | 20 | 40 | 20 | 10 |
| 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| P(k2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.076 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com