|
|
|
设F1,F2分别是椭圆E:x2+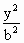 =10(0<b<1)的左、右焦点,过点F1的直线交椭圆E于A,B两点,若|AF1|=3|BF1|,AF2⊥x轴,则椭圆E的方程为________. =10(0<b<1)的左、右焦点,过点F1的直线交椭圆E于A,B两点,若|AF1|=3|BF1|,AF2⊥x轴,则椭圆E的方程为________.
|
|
|
答案:
解析:
|
答案:
解析:此题以椭圆知识运用为背景,考察数形结合思想、方程思想的运用意识,其中含有解题策略运用.
|
练习册系列答案
相关习题
科目:高中数学
来源:人教B版(新课标) 必修2
题型:
|
|
|
已知直线l:x=my+4(m∈R)与x轴交于点P,交抛物线y2=2ax(a>0)于A,B两点,点Q是点P关于坐标原点O的对称点,记直线AQ,BQ的斜率分别为k1,k2.
(Ⅰ)若P为抛物线的焦点,求a的值,并确定抛物线的准线与以AB为直径的圆的位置关系.
(Ⅱ)试证明:k1+k2为定值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:苏教版(新课标) 选修1-1
题型:
|
|
|
已知双曲线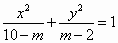 的实轴在y轴上且焦距为8,则双曲线的渐近线的方程为 的实轴在y轴上且焦距为8,则双曲线的渐近线的方程为
|
| [ ] |
A. |
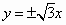
|
B. |
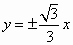
|
C. |
y=±3x
|
D. |
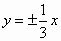
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
“x<0”是“ln(x+1)<0”的
|
| [ ] |
A. |
充分不必要条件
|
B. |
必要不充分条件
|
C. |
充分必要条件
|
D. |
既不充分也不必要条件
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若函数f(x)=|x+1|+|2x+a|的最小值为3,则实数a的值为
|
| [ ] |
A. |
5或8
|
B. |
-1或5
|
C. |
-1或-4
|
D. |
-4或8
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图,已知两条抛物线E1:y2=2p1x(p1>0)和E2:y2=2p2x(p2>0),过原点O的两条直线l1和l2,l1与E1,E2分别交于A1,A2两点,l2与E1,E2分别交于B1,B2两点.
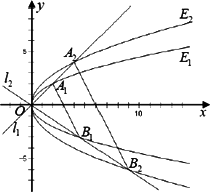
(1)证明:A1B1∥A2B2;
(2)过原点O作直线(异于l1,l2)与E1,E2分别交于C1,C2两点.记?A1B1C1与的△A2B2C2面积分别为S1与S2,求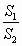 的值. 的值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
函数y=ln(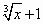 )(x>-1)的反函数是 )(x>-1)的反函数是
|
| [ ] |
A. |
y=(1-ex)3(x>-1)
|
B. |
y=(ex-1)3(x>-1)
|
C. |
y=(1-ex)3(x∈R)
|
D. |
y=(ex-1)3(x∈R)
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知抛物线C:y2=2px(p>0)的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且 . .
(1)求抛物线C的方程;
(2)过F的直线l与C相交于A,B两点,若AB的垂直平分线 与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程. 与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知函数f(x)=xcosx-sinx+1(x>0).
(1)求f(x)的单调区间;
(2)记xi为f(x)的从小到大的第i(i∈N*)个零点,证明:对一切n∈N*,有 . .
|
|
|
查看答案和解析>>

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案