
已知数列 的前
的前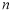 项和为
项和为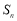 ,
,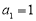 ,
,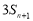 是
是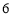 与
与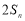 的等差中项(
的等差中项(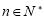 ).
).
(1)求数列 的通项公式;
的通项公式;
(2)是否存在正整数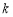 ,使不等式
,使不等式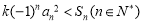 恒成立,若存在,求出
恒成立,若存在,求出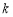
的最大值;若不存在,请说明理由.
(1) 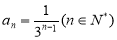 (2)存在,11
(2)存在,11
【解析】
试题分析:
(1) 解法一:根据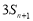 是
是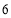 与
与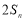 的等差中项,利用等差中项得到
的等差中项,利用等差中项得到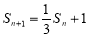 ,(
,(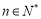 )①,
)①,
当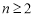 时有
时有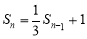 ②, 则 ①-②可得
②, 则 ①-②可得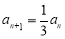 ,从而可得数列通项.
,从而可得数列通项.
解法二: 根据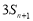 是
是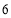 与
与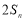 的等差中项,利用等差中项得到
的等差中项,利用等差中项得到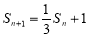 ,(
,(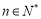 )①,根据该式的结构特征,利用构造法,可构造出等比数列
)①,根据该式的结构特征,利用构造法,可构造出等比数列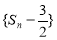 ,从而求得
,从而求得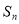 ,进而利用
,进而利用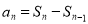 得到数列的通项.
得到数列的通项.
(2)根据(1)的结论可知,数列是等比数列,所以可以得到其前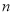 项和;代入
项和;代入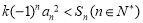 化简,讨论
化简,讨论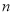 的奇偶发现,
的奇偶发现, 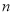 为奇数时,恒成立;
为奇数时,恒成立; 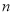 为偶数时,可将其转化为二次函数在固定区间恒成立问题,利用单调性可判断是否存在这样的正整数
为偶数时,可将其转化为二次函数在固定区间恒成立问题,利用单调性可判断是否存在这样的正整数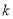 .
.
试题解析:(1)解法一:因为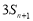 是
是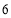 与
与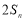 的等差中项,
的等差中项,
所以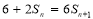 (
(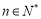 ),即
),即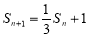 ,(
,(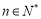 )①
)①
当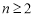 时有
时有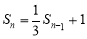 ②
②
①-②得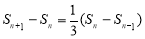 ,即
,即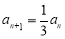 对
对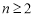 都成立
都成立
又根据①有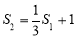 即
即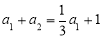 ,所以
,所以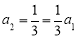
所以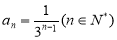 . 所以数列
. 所以数列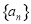 是首项为1,公比为
是首项为1,公比为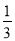 的等比数列.
的等比数列.
解法二: 因为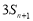 是
是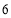 与
与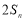 的等差中项,
的等差中项,
所以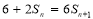 (
(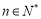 ),即
),即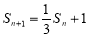 ,(
,(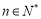 )
)
由此得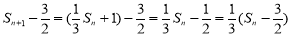 (
(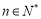 ),
),
又 ,所以
,所以  (
(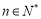 ),
),
所以数列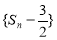 是以
是以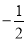 为首项,
为首项,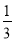 为公比的等比数列.
为公比的等比数列.
得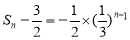 ,即
,即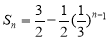 (
(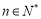 ),
),
所以,当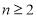 时,
时,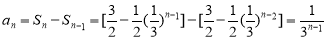 ,
,
又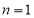 时,
时,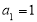 也适合上式, 所以
也适合上式, 所以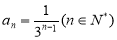 .
.
(2)根据(1)的结论可知,
数列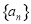 是首项为1,公比为
是首项为1,公比为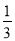 的等比数列,
的等比数列,
所以其前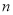 项和为
项和为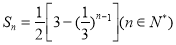 .
.
原问题等价于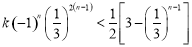 (
(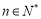 )①恒成立.
)①恒成立.
当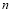 为奇数时,不等式左边恒为负数,右边恒为正数,所以对任意正整数
为奇数时,不等式左边恒为负数,右边恒为正数,所以对任意正整数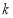 不等式恒成立;
不等式恒成立;
当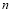 为偶数时,①等价于
为偶数时,①等价于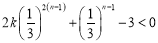 恒成立,
恒成立,
令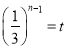 ,有
,有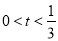 ,则①等价于
,则①等价于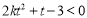 在
在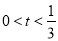 恒成立,
恒成立,
因为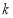 为正整数,二次函数
为正整数,二次函数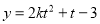 的对称轴显然在
的对称轴显然在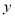 轴左侧,
轴左侧,
所以当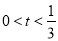 时,二次函数为增函数,故只须
时,二次函数为增函数,故只须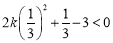 ,解得
,解得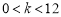 ,
,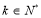 ,
,
所以存在符合要求的正整数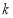 ,且其最大值为11.
,且其最大值为11.
考点:等差中项;利用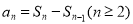 求通项;构造等比数列法;分类讨论;二次函数在固定区间恒成立.
求通项;构造等比数列法;分类讨论;二次函数在固定区间恒成立.


 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:高中数学 来源:2016届浙江省高一下学期期中数学试卷(解析版) 题型:填空题
 在
在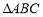 中,内角
中,内角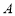 、
、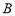 、
、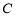 所对的边分别为
所对的边分别为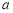 、
、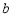 、
、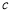 ,给出下列命题:
,给出下列命题:
①若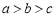 ,则
,则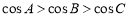 ;
;
②若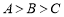 ,则
,则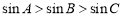 ;
;
③若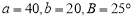 ,则
,则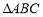 有两解;
有两解;
④必存在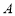 、
、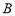 、
、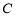 ,使
,使 成立.
成立.
其中,正确命题的编号为 .(写出所有正确命题的编号)
查看答案和解析>>
科目:高中数学 来源:2016届浙江省高一下学期期中数学试卷(解析版) 题型:选择题
在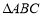 中,已知
中,已知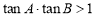 ,则
,则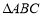 是( )
是( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.最小内角大于45°的三角形
查看答案和解析>>
科目:高中数学 来源:2016届浙江省等三校高一下学期第二次联考数学试卷(解析版) 题型:解答题
在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA=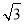 acosB.
acosB.
(1)求角B的大小;
(2)若b=3,sinC=2sinA,求a,c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com