
【题目】已知向量![]() ,
,![]() ,
,![]() ,向量
,向量![]() 与
与![]() 垂直,且
垂直,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)向量![]() 与
与![]() 垂直,得
垂直,得![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列,利用等比数列的通项公式可求
为公比的等比数列,利用等比数列的通项公式可求![]() ;(2)由
;(2)由![]() ,则
,则![]() ,利用错位相减法可求其和.
,利用错位相减法可求其和.
试题解析:(1)∵向量![]() 与
与![]() 垂直,∴
垂直,∴![]() ,即∴
,即∴![]() ,∴
,∴![]()
∴![]() 是以1为首项,2为公比的等比数列,∴
是以1为首项,2为公比的等比数列,∴![]() .
.
(2)∵![]() ,∴
,∴![]()
∴![]() ,∴
,∴![]() ,①
,①
∴![]() ,②
,②
∴由①![]() ②得,
②得,![]()
∴![]() .
.
【 方法点睛】本题主要考查等比数列通项、平面向量数量积公式以及错位相减法求数列的通项,属于中档题.一般地,如果数列![]() 是等差数列,
是等差数列,![]() 是等比数列,求数列
是等比数列,求数列![]() 的前
的前![]() 项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列
项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列![]() 的公比,然后作差求解, 在写出“
的公比,然后作差求解, 在写出“![]() ”
”![]() 与“
与“![]() ” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“
” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“![]() ”的表达式.
”的表达式.


科目:高中数学 来源: 题型:
【题目】【2017届河北省正定中学高三上学期第三次月考(期中)数学(理)】在平面直角坐标系中,当![]() 不是原点时,定义
不是原点时,定义![]() 的“伴随点”为
的“伴随点”为![]() ;当
;当![]() 是原点时,定义
是原点时,定义![]() 的“伴随点”为它自身,平面曲线
的“伴随点”为它自身,平面曲线![]() 上所有点的“伴随点”所构成的曲线
上所有点的“伴随点”所构成的曲线![]() 定义为曲线
定义为曲线![]() 的“伴随曲线”,现有下列命题:
的“伴随曲线”,现有下列命题:
①若点![]() 的“伴随点”是点
的“伴随点”是点![]() ,则点
,则点![]() 的“伴随点”是点
的“伴随点”是点![]() ;
;
②若曲线![]() 关于
关于![]() 轴对称,则其“伴随曲线”
轴对称,则其“伴随曲线” ![]() 关于
关于![]() 轴对称;
轴对称;
③单位圆的“伴随曲线”是它自身;
④一条直线的“伴随曲线”是一条直线.
其中真命题的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 是过点
是过点![]() ,倾斜角为
,倾斜角为![]() 的直线,以直角坐标系
的直线,以直角坐标系![]() 的原点为极点,
的原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的一个参数方程;
的一个参数方程;
(2)曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地政府决定建造一批保障房供给社会,缓解贫困人口的住房问题,计划用1 600万元购得一块土地,在该土地上建造10幢楼房的住宅小区,每幢楼的楼层数相同,且每层建筑面积均为1 000平方米,每平方米的建筑费用与楼层有关,第x层楼房每平方米的建筑费用为(kx+800)元(其中k为常数).经测算,若每幢楼为5层,则该小区每平方米的平均综合费用为1 270元.
注:每平方米平均综合费用=![]() .
.
(1) 求k的值;
(2) 问要使该小区楼房每平方米的平均综合费用最低,应将这10幢楼房建成多少层?此时每平方米的平均综合费用为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(Ⅱ)设![]() ,
,![]() ,(
,(![]() 为自然对数的底数).是否存在常数
为自然对数的底数).是否存在常数![]() ,使
,使![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医药研究所开发的一种药,如果成年人按规定的剂量服用,据监测,服药后每毫升中的含药量![]() (微克)与时间
(微克)与时间![]() (小时)之间近似满足如图所示的曲线.(当
(小时)之间近似满足如图所示的曲线.(当![]() 时,
时, ![]() ).
).
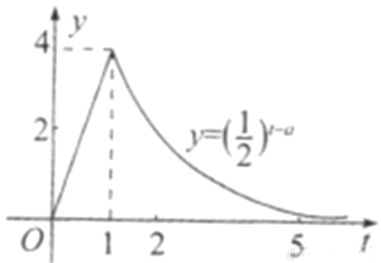
(1)写出第一次服药后![]() 与
与![]() 之间的函数关系式
之间的函数关系式![]() ;
;
(2)据进一步测定,每毫升血液中含药量不少于![]() 微克时,治疗疾病有效,求服药一次后治疗疾病有效时间.
微克时,治疗疾病有效,求服药一次后治疗疾病有效时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域是R,对于任意实数
的定义域是R,对于任意实数![]() ,恒有
,恒有![]() ,且当
,且当![]() 时,
时, ![]() 。
。
(1)求证: ![]() ,且当
,且当![]() 时,有
时,有![]() ;
;
(2)判断![]() 在R上的单调性;
在R上的单调性;
(3)设集合A=![]() ,B=
,B=![]() ,若A∩B=
,若A∩B=![]() ,求
,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个顶点分别为
的两个顶点分别为![]() ,焦点在
,焦点在![]() 轴上,离心率为
轴上,离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
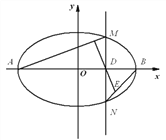
(Ⅱ)点![]() 为
为![]() 轴上一点,过
轴上一点,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于不同的两点
于不同的两点![]() ,过
,过![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() .求
.求![]() 与
与![]() 的面积之比.
的面积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某DVD光盘销售部每天的房租、人员工资等固定成本为300元,每张DVD光盘的进价是6元,销售单价与日均销售量的关系如表所示:
销售单价(元) | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
日均销售量(张) | 480 | 440 | 400 | 360 | 320 | 280 | 240 |
(1)请根据以上数据作出分析,写出日均销售量P(x)(张)关于销售单价x(元)的函数关系式,并写出其定义域;
(2)问这个销售部销售的DVD光盘销售单价定为多少时才能使日均销售利润最大?最大销售利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com