【答案】
分析:(1)根据f
n(x)=
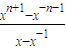
,y=x+
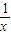
,代入yf
n(x)-f
n-1(x),化简即可得证;
(2)先证明命题对n=1,2成立,再设n≤m(m≥2,m为正整数,命题成立,现证命题对于n=m+1成立,分类讨论:①m为偶数,则m+1为奇数;②若m为奇数,则m+1为偶数,由归纳假设,即可证得结论.
解答:证明:(1)∵f
n(x)=
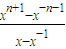
,y=x+
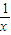
∴yf
n(x)-f
n-1(x)=(x+
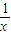
)×
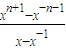
-
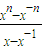
=
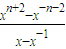
=f
n+1(x)
(2)f
1(x)=x+
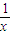
,f
2(x)=x
2+1+x
-2=y
2-1,故命题对n=1,2成立
设n=m(m≥2,m为正整数,命题成立,现证命题对于n=m+1成立
①m为偶数,则m+1为奇数,由归纳假设知,对于n=m及n=m-1,有
f
m(x)=y
m-
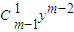
+…+…+(-1)
i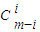
y
m-2i+…+
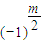
①
f
m-1(x)=y
m-1-
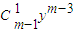
+…+(-1)
i-1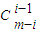
y
m+1-2i+…+
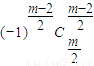
y ②
∴yf
m(x)-f
m-1(x)=y
m+1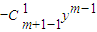
+…+(-1)
i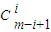
y
m+1-2i+…+
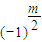
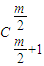
y
即命题对n=m+1成立.
②若m为奇数,则m+1为偶数,由归纳假设知,对于n=m及n=m-1,有
f
m(x)=y
m-1-
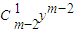
+…+…+(-1)
i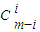
y
m-2i+…+
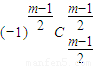
y③
f
m-1(x)=y
m-1-

+…+(-1)
i-1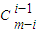
y
m+1-2i+…+
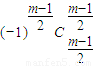
④
用y乘③减去④,同上合并,并注意最后一项常数项为-
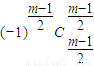
=
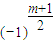
.
于是得到yf
m(x)-f
m-1(x)=y
m+1-C
m1y
m-1+…+
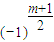
,即仍有对于n=m+1,命题成立
综上所述,知对于一切正整数n,命题成立.
点评:本题考查数学归纳法,考查分类讨论的数学思想,考查学生的计算能力,难度较大.

 (x≠0,±1),令y=x+
(x≠0,±1),令y=x+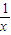 .
.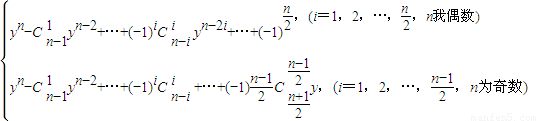 .
.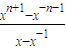 ,y=x+
,y=x+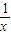 ,代入yfn(x)-fn-1(x),化简即可得证;
,代入yfn(x)-fn-1(x),化简即可得证;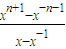 ,y=x+
,y=x+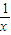
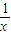 )×
)×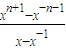 -
-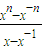 =
=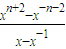 =fn+1(x)
=fn+1(x)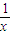 ,f2(x)=x2+1+x-2=y2-1,故命题对n=1,2成立
,f2(x)=x2+1+x-2=y2-1,故命题对n=1,2成立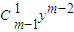 +…+…+(-1)i
+…+…+(-1)i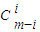 ym-2i+…+
ym-2i+…+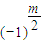 ①
①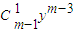 +…+(-1)i-1
+…+(-1)i-1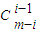 ym+1-2i+…+
ym+1-2i+…+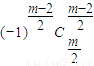 y ②
y ②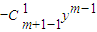 +…+(-1)i
+…+(-1)i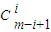 ym+1-2i+…+
ym+1-2i+…+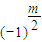
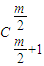 y
y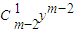 +…+…+(-1)i
+…+…+(-1)i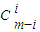 ym-2i+…+
ym-2i+…+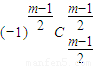 y③
y③ +…+(-1)i-1
+…+(-1)i-1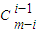 ym+1-2i+…+
ym+1-2i+…+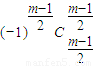 ④
④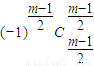 =
=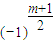 .
.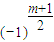 ,即仍有对于n=m+1,命题成立
,即仍有对于n=m+1,命题成立

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案