练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某射击小组有甲、乙、丙三名射手，已知甲击中目标的概率是，甲、丙二人都没有击中目标的概率是，乙、丙二人都击中目标的概率是.甲乙丙是否击中目标相互独立.

    （1）求乙、丙二人各自击中目标的概率；

    （2）设乙、丙二人中击中目标的人数为X，求X的分布列和数学期望.

    【答案】（1），.（2）分布列见解析，数学期望.

    【解析】

    （1）设甲、乙、丙击中目标分别记为事件，则，且，由此能求出乙、丙二人各自击中目标的概率．
    （2）由题意X的可能取值为0，1，2，分别求出相应的概率，由此能求出X的分布列和E（X）．

    解：（1）设甲、乙、丙击中目标分别记为事件A、B、C，则，且有

    即

    解得，，

    所以乙、丙二人各自击中目标的概率分别为，；

    （2）由题意，X的可能取值为0，1，2，

    ，

    ，

    .

    所以随机变量X的分布列为

    X

    0

    1

    2

    P

    所以X的数学期望为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，三棱柱中，侧面是菱形，其对角线的交点为，且，.

    （1）求证：平面；

    （2）设，若直线与平面所成的角为，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校象棋社团组织中国象棋比赛,采用单循环赛制,即要求每个参赛选手必须且只须和其他选手各比赛一场,胜者得分,负者得分,平局两人各得分.若冠军获得者得分比其他人都多,且获胜场次比其他人都少,则本次比赛的参赛人数至少为

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数满足，且当时，成立，若，，，则a，b，c的大小关系是()

    A. aB. C. D. c

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列的前项和满足，.数列的前项和为，则满足的最小的值为______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，其中e为自然对数的底数.

    （1）当a＝0时，求函数f (x)的单调减区间；

    （2）已知函数f (x)的导函数f (x)有三个零点x1，x2，x3(x1 x2 x3).①求a的取值范围；②若m1，m2(m1 m2)是函数f (x)的两个零点，证明：x1m1x1 1.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，直线l的参数方程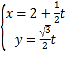(t为参数)，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为：．

    Ⅰ直线l的参数方程化为极坐标方程；

    Ⅱ求直线l与曲线C交点的极坐标其中，．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若是的极小值点，求实数的取值范围；

    （2）若，证明：当时，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在某校举行的航天知识竞赛中，参与竞赛的文科生与理科生人数之比为，且成绩分布在，分数在以上（含）的同学获奖. 按文理科用分层抽样的方法抽取人的成绩作为样本，得到成绩的频率分布直方图（见下图）.

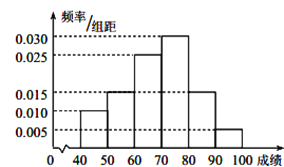
    （I）在答题卡上填写下面的列联表，能否有超过的把握认为“获奖与学生的文理科有关”？

    文科生

    理科生

    合计

    获奖

    不获奖

    合计

    （II）将上述调査所得的频率视为概率，现从该校参与竞赛的学生中，任意抽取名学生，记“获奖”学生人数为，求的分布列及数学期望.

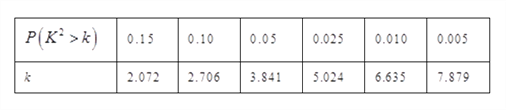
    附表及公式：，其中.

    查看答案和解析>>

    同步练习册答案