【题目】在平面直角坐标系xOy中，直线l的参数方程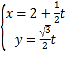
(t为参数)，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为：
．
Ⅰ
直线l的参数方程化为极坐标方程；
Ⅱ求直线l与曲线C交点的极坐标其中
，
．
科目：高中数学 来源： 题型：
【题目】已知幂函数f（x）＝（3m2﹣2m）x
在（0，+∞）上单调递增，g（x）＝x2﹣4x+t.
（1）求实数m的值；
（2）当x∈[1，9]时，记f（x），g（x）的值域分别为集合A，B，设命题p：x∈A，命题q：x∈B，若命题q是命题p的必要不充分条件，求实数t的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
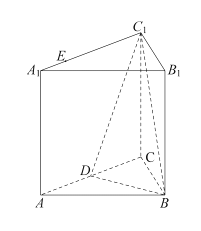
【题目】如图，正三棱柱
的所有棱长都为
是
的中点，
在
边上，
.
（1）证明:平面
平面
；
（2）若
是侧面
内的动点，且
平面
.
①在答题卡中作出点的轨迹，并说明轨迹的形状(不需要说明理由)；
②求二面角
的余弦值的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某射击小组有甲、乙、丙三名射手，已知甲击中目标的概率是
，甲、丙二人都没有击中目标的概率是
，乙、丙二人都击中目标的概率是
.甲乙丙是否击中目标相互独立.
（1）求乙、丙二人各自击中目标的概率；
（2）设乙、丙二人中击中目标的人数为X，求X的分布列和数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，
为抛物线
上不同的两点，且
，点
且
于点.
（1）求
的值；
（2）过
轴上一点 
的直线
交
于
，
两点，
在的准线上的射影分别为
，
为的焦点，若
，求
中点
的轨迹方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】10名象棋选手进行单循环赛（即每两名选手比赛一场）．规定两人对局胜者得2分，平局各得1分，负者得0分，并按总得分由高到低进行排序．比赛结束后，10名选手的得分各不相同，且第二名的得分是最后五名选手得分之和的
．则第二名选手的得分是____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
