
已知向量a=
 ,b=
,b= ,c=
,c= ,
,
(1)求证:(a+b)⊥(a-b);
(2)设函数
 ,求
,求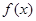 的最大值和最小值.[来
的最大值和最小值.[来
(2)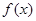 的最大值为4,最小值为0.
的最大值为4,最小值为0.
【解析】(1)计算向量的数量积;(2)将f(x)化为 4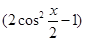 . 再由x∈
. 再由x∈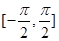 ,
得
,
得 ∈
∈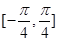 求解.
求解.
解:(1)【解法一】依题意得:a+b=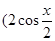 ,
,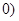 ,a-b=
,a-b=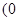 ,
,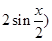
∴(a+b)·(a-b)=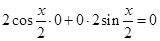 ,
,
∴(a+b)⊥(a-b). (5分)
【解法二】依题意得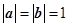 ,∴(a+b)·(a-b)=
,∴(a+b)·(a-b)=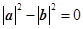 ,
,
∴(a+b)⊥(a-b). (5分)
(2)依题意得a+c=(cos +1,sin
+1,sin -1),b+c=(cos
-1),b+c=(cos +1,-sin
+1,-sin -1),
-1),
∴|a+c|2-3=(cos +1)2+(sin
+1)2+(sin -1)2-3=2cos
-1)2-3=2cos -2sin
-2sin ,
,
|b+c|2-3=(cos +1)2+(-sin
+1)2+(-sin -1)2-3=2cos
-1)2-3=2cos +2sin
+2sin ,
,
∴f(x)=(|a+c|2-3)(|b+c|2-3)=(2cos -2sin
-2sin )(2cos
)(2cos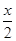 +2sin
+2sin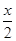 )
)
=4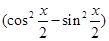 =4
=4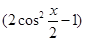 . 又x∈
. 又x∈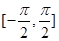 ,
∴
,
∴ ∈
∈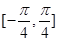
故当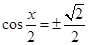 ,即
,即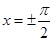 时,
时,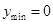 ;当
;当 ,即
,即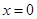 时,
时,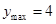
∴函数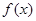 的最大值为4,最小值为0.
(12分)
的最大值为4,最小值为0.
(12分)


科目:高中数学 来源:高考总复习全解 数学 一轮复习·必修课程 (人教实验版) B版 人教实验版 B版 题型:044
已知向量a=![]() ,b=
,b=![]() 且
且
x∈[0,![]() ],求:
],求:
(1)a·b及|a+b|;(2)若f(x)=a·b-2λ|a+b|的最小值是-![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
科目:高中数学 来源:吉林省白山二中2012届高三第二次月考数学文科试题 题型:013
已知向量a=![]() ,b=(0,-1),c=
,b=(0,-1),c=![]() .若a-2b与c共线,则k=
.若a-2b与c共线,则k=
A.1
B.![]()
C.-1
D.3
查看答案和解析>>
科目:高中数学 来源:2013-2014学年上海交大附中高三数学理总复习二三角恒等变换与解三角形练习卷(解析版) 题型:选择题
已知向量a= ,b=(4,4cos α-
,b=(4,4cos α- ),若a⊥b,则sin
),若a⊥b,则sin 等于( )
等于( )
A.- B.-
B.-
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com