
| 1 |
| a |
| 2n+1 |
| n+1 |
| 1 |
| n+1 |
| 1 |
| a |
| 3 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:高中数学 来源: 题型:
| ax+2 |
| x+b |
| 2 |
| f(an)-1 |
| Sn |
| (n-1)•2n |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| π |
| 2 |
| π |
| 2 |
| 1 |
| 2n |
| i-1 |
| 2n |
| i+1 |
| 2n |
| i |
| 2n-1 |
查看答案和解析>>
科目:高中数学 来源:2013年上海市浦东新区高考数学一模试卷(理科)(解析版) 题型:解答题
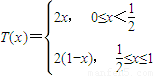
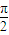 x))和y=sin(
x))和y=sin(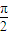 T(x))的解析式;
T(x))的解析式;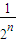 ]时,求y=Tn(x)的解析式;
]时,求y=Tn(x)的解析式;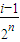 ,
,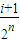 ](i∈N*,1≤i≤2n-1)时,都有Tn(x)=Tn(
](i∈N*,1≤i≤2n-1)时,都有Tn(x)=Tn(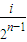 -x)恒成立.
-x)恒成立.查看答案和解析>>
科目:高中数学 来源:高考数学一轮复习必备(第85课时):第十章 排列、组合和概率-二项式定理(2)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com