
定义在 上的函数
上的函数 ,满足
,满足 ,
,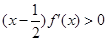 ,若
,若 且
且 ,则有( ).
,则有( ).
A. | B. | C. | D.不能确定 |
A
解析试题分析:根据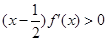 确定函数的单调性,根据f(1-x)=f(x),可得f(x)关于x=
确定函数的单调性,根据f(1-x)=f(x),可得f(x)关于x= 对称,进一步分类讨论x1与在x2的位置关系,即可得到f(x1)<f(x2).解:因为
对称,进一步分类讨论x1与在x2的位置关系,即可得到f(x1)<f(x2).解:因为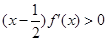 ,则可知当x>
,则可知当x> 时,,f′(x)>0,函数单调增,x<
时,,f′(x)>0,函数单调增,x< 时,f′(x)<0,函数单调减,故可知函数f(1-x)=f(x),可知函数在①x1在对称轴x=
时,f′(x)<0,函数单调减,故可知函数f(1-x)=f(x),可知函数在①x1在对称轴x= 的右边或在对称轴上,由x1<x2,易得f(x1)<f(x2);②x1在对称轴x=
的右边或在对称轴上,由x1<x2,易得f(x1)<f(x2);②x1在对称轴x= 的左边,由x1+x2>3易得x2>
的左边,由x1+x2>3易得x2> ,∴x2在对称轴x=
,∴x2在对称轴x= 的右边.因为|x2-
的右边.因为|x2- >
>  - x1,即|x2-
- x1,即|x2- |>|
|>| -x1|,∴f(x1)<f(x2)综合可得:f(x1)<f(x2)故选A.
-x1|,∴f(x1)<f(x2)综合可得:f(x1)<f(x2)故选A.
考点:函数的单调性
点评:本题考查函数的单调性,考查函数的对称性,正确运用函数的单调性与对称性是关键.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:单选题
如图,函数y=f(x)的图象为折线ABC,设f 1 (x)=f(x),f n+1 (x)=f [f n(x)],n∈N*,则函数y=f 4 (x)的图象为

A. B. 
C. D.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
定义在R上的函数 ,对任意不等的实数
,对任意不等的实数 都有
都有 成立,又函数
成立,又函数 的图象关于点(1,0)对称,若不等式
的图象关于点(1,0)对称,若不等式 成立,则当1≤x<4时,
成立,则当1≤x<4时, 的取值范围是
的取值范围是
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知函数 的定义域为
的定义域为 ,部分对应值如下表。
,部分对应值如下表。 的导函数
的导函数 的图像如图所示。
的图像如图所示。
 |  | 0 |  |  | 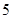 |
 |  | 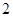 |  | 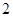 |  |

 的命题:
的命题: 在
在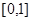 上是减函数;②如果当
上是减函数;②如果当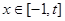 时,
时, 最大值是
最大值是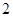 ,那么
,那么 的最大值为
的最大值为 ;③函数
;③函数 有
有 个零点,则
个零点,则 ;④已知
;④已知 是
是 的一个单调递减区间,则
的一个单调递减区间,则 的最大值为
的最大值为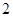 。
。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com