
(本小题满分12分)某企业投入81万元经销某产品,经销时间共60个月,市场调研表明,该企业在经销这个产品期间第 个月的利润
个月的利润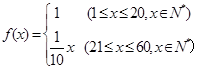 (单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第
(单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第 个月的当月利润率
个月的当月利润率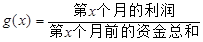 ,例如:
,例如: .
.
(Ⅰ) 求
求 ; (Ⅱ)求第
; (Ⅱ)求第 个月的当月利润率
个月的当月利润率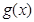 ;
;
(Ⅲ)该企业经销此产品期间,哪个月的当月利润率最大,并求该月的当月利润率.
 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:解答题
(本小题满分13分)
(本小题满分12分)某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场,其总面积为3000平方米,其中场地四周(阴影部分)为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为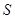 平方米.
平方米.
(1)分别写出用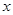 表示
表示 和用
和用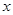 表示
表示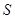 的函数关系式(写出函数定义域);
的函数关系式(写出函数定义域);
(2)怎样设计能使S取得最大值,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分) 商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少。把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元。现在这种羊毛衫的成本价是100元/ 件,商场以高于成本价的相同价格(标价)出售. 问:
(Ⅰ)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(Ⅱ)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分13分)
已知函数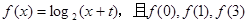 成等差数列,点
成等差数列,点 是函数
是函数 图像上任意一点,点
图像上任意一点,点 关于原点的对称点
关于原点的对称点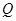 的轨迹是函数
的轨迹是函数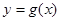 的图像。
的图像。
(1)解关于 的不等式
的不等式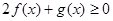 ;
;
(2)当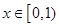 时,总有
时,总有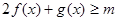 恒成立,求
恒成立,求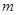 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com