
雾霾大气严重影响人们生活,某科技公司拟投资开发新型节能环保产品,策划部制定投资计划时,不仅要考虑可能获得的盈利,而且还要考虑可能出现的亏损,经过市场调查,公司打算投资甲、乙两个项目,根据预测,甲、乙项目可能的最大盈利率分别为100%和60%,可能的最大亏损率分别为20%和10%,投资人计划投资金额不超过10万元要求确保可能的资金亏损不超过1.6万元.
(1)若投资人用 万元投资甲项目,
万元投资甲项目, 万元投资乙项目,试写出
万元投资乙项目,试写出 、
、 所满足的条件,并在直角坐标系内做出表示
所满足的条件,并在直角坐标系内做出表示 、
、 范围的图形;
范围的图形;
(2)根据(1)的规划,投资公司对甲、乙两个项目投资多少万元,才能是可能的盈利最大?
(1)如图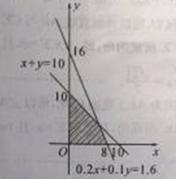 ;
;
(2)用6万元投资甲项目,4万元投资乙项目.
解析试题分析:(1)根据已知条件列出不等式组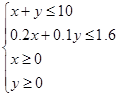 ,再在平面直角坐标系中画出对应的可行域,注意边界上的点也满足条件;(2)主要是利用可行域求解线性目标函数的最大值即得投资公司获得的最大利润,图解法解决含有实际背景的线性规划问题的基本步骤是:①列出约束条件,确定目标函数;②画出不等式(组)表示的平面区域;③作平行直线系使之与可行域有交点,求得最优解;④写出目标函数的最值,并下结论.
,再在平面直角坐标系中画出对应的可行域,注意边界上的点也满足条件;(2)主要是利用可行域求解线性目标函数的最大值即得投资公司获得的最大利润,图解法解决含有实际背景的线性规划问题的基本步骤是:①列出约束条件,确定目标函数;②画出不等式(组)表示的平面区域;③作平行直线系使之与可行域有交点,求得最优解;④写出目标函数的最值,并下结论.
试题解析:(1)由题意,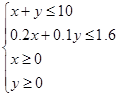 上述不等式组表示的平面区域如图中阴影部分(含边界),
上述不等式组表示的平面区域如图中阴影部分(含边界),
根据(1)的规划和题设条件,可知目标函数为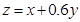 ,作直线
,作直线 ,并作平行于直线
,并作平行于直线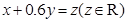 与可行域相交,当平行直线经过直线
与可行域相交,当平行直线经过直线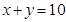 与
与 的交点
的交点 时,其截距最大,解方程组
时,其截距最大,解方程组 ,解得
,解得 ,即
,即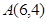 ,
,
此时 (万元),
(万元),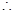 当
当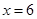 ,
,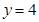 时,
时, 取得最大值.
取得最大值.
即投资人用6万元投资甲项目,4万元投资乙项目,才能确保亏损不超过1.6万元,使可能的利润最大.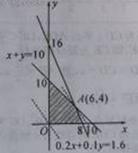
考点:用线性规划解决实际问题,投资利润最大问题.


科目:高中数学 来源: 题型:解答题
一农民有基本农田2亩,根据往年经验,若种水稻,则每季亩产量为400公斤;若种花生,则每季亩产量为100公斤.但水稻成本较高,每季每亩240元,而花生只需80元;且花生每公斤卖5元,稻米每公斤卖3元.现该农民手头有400元,两种作物各种多少,才能获得最大收益?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司计划2014年在A,B两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元.A,B两个电视台的广告收费标准分别为500元/分钟和200元/分钟,假定A,B两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在两个电视台做广告的时间,才能使公司的收益最大?最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某营养师要为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物、6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物、6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物、42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某厂生产甲、乙两种产品每吨所需的煤、电和产值如下表所示.
但国家每天分配给该厂的煤、电有限, 每天供煤至多56吨,供电至多450千瓦,问该厂如何安排生产,使得该厂日产值最大?最大日产值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
在一个居民小区内设计一个边长为5米的菱形喷水池,规划要求菱形的一条对角线长
不大于6米,另一条长 不小于6米,则菱形喷水池的两条对角线的长度之和
不小于6米,则菱形喷水池的两条对角线的长度之和 的
的
最大值为 米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com