
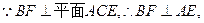
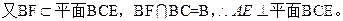
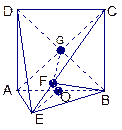
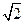 ,
,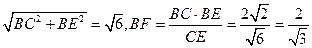
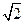 ,在直角三角形BFG中,
,在直角三角形BFG中,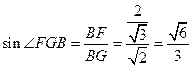
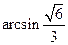
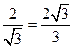
 交AB于点O. OE=1.
交AB于点O. OE=1.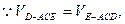
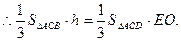
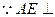 平面BCE,
平面BCE,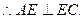

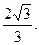
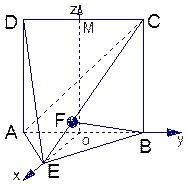
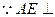 面BCE,BE
面BCE,BE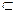 面BCE,
面BCE,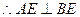 ,
,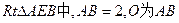 的中点,
的中点,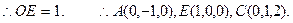
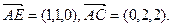 设平面AEC的一个法向量为
设平面AEC的一个法向量为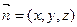 ,
,
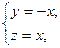
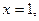 得
得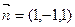 是平面AEC的一个法向量.
是平面AEC的一个法向量.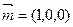 ,
,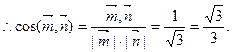
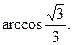
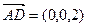 ,
,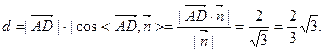


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源:不详 题型:解答题
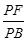 =
=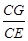 =λ∈(0,1).
=λ∈(0,1).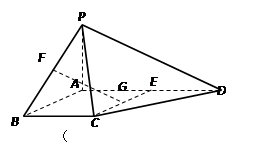
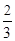 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
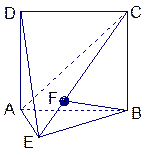
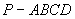 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱 底面ABCD,
底面ABCD,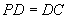 ,E是PC的中点,作
,E是PC的中点,作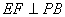 交PB于点F;
交PB于点F; 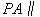 平面
平面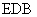 ;
; 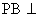 平面EFD;
平面EFD;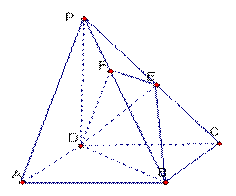
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
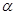 、
、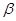 表示两个不同的平面,
表示两个不同的平面, 、
、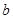 表示两条不同的直线,则下列命题正确的是( )
表示两条不同的直线,则下列命题正确的是( )A.若 ⊥ ⊥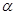 , ,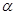 ⊥ ⊥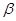 ,则 ,则 ∥ ∥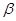 | B.若 ∥ ∥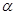 , , ∥ ∥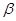 ,则 ,则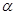 ∥ ∥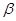 |
C.若 ⊥ ⊥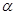 , ,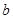 ⊥ ⊥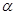 ,则 ,则 ∥ ∥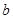 | D.若 ⊥ ⊥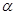 , , ⊥ ⊥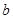 ,则 ,则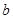 ∥ ∥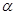 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
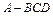 中,三条棱
中,三条棱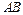 、
、 、
、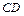 两两垂直,且
两两垂直,且 与平面
与平面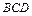 成
成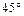 角,与平面
角,与平面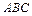 成
成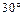 角.
角.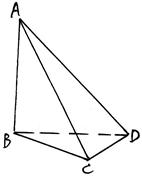
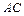 与平面
与平面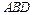 所成角的大小;
所成角的大小;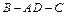 大小的余弦值.
大小的余弦值.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
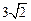 ,且DA,DB,DC两两互相垂直,
,且DA,DB,DC两两互相垂直,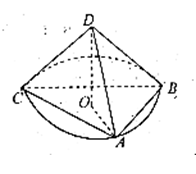
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com