
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,若向量 ![]() =(﹣cosB,sinC),
=(﹣cosB,sinC), ![]() =(﹣cosC,﹣sinB),且
=(﹣cosC,﹣sinB),且 ![]() . (Ⅰ)求角A的大小;
. (Ⅰ)求角A的大小;
(Ⅱ)若b+c=4,△ABC的面积 ![]() ,求a的值.
,求a的值.
【答案】解:(Ⅰ)∵ ![]() =(﹣cosB,sinC),
=(﹣cosB,sinC), ![]() =(﹣cosC,﹣sinB),
=(﹣cosC,﹣sinB),
∴ ![]() ,即
,即 ![]() ,
,
∵A+B+C=π,∴B+C=π﹣A,可得cos(B+C)= ![]() ,
,
即 ![]() ,结合A∈(0,π),可得
,结合A∈(0,π),可得 ![]() .
.
(Ⅱ)∵△ABC的面积 ![]() =
= ![]() =
= ![]() ,
, ![]()
∴ ![]() ,可得bc=4.
,可得bc=4.
又由余弦定理得: ![]() =b2+c2+bc,
=b2+c2+bc,
∴a2=(b+c)2﹣bc=16﹣4=12,解之得 ![]() (舍负).
(舍负).
【解析】(Ⅰ)由向量数量积的坐标运算公式,结合 ![]() 算出
算出 ![]() ,利用三角形内角和定理和π﹣α的诱导公式可得
,利用三角形内角和定理和π﹣α的诱导公式可得 ![]() ,结合A∈(0,π)即可算出角A的大小;
,结合A∈(0,π)即可算出角A的大小;
(Ⅱ)根据正弦定理的面积公式,结合△ABC的面积为 ![]() 算出bc=4. 再用余弦定理a2=b2+c2﹣2bccosA的式子,代入数据即可算出a2=12,从而可得
算出bc=4. 再用余弦定理a2=b2+c2﹣2bccosA的式子,代入数据即可算出a2=12,从而可得 ![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x﹣8,g(x)=2x2﹣4x﹣16,
(1)求不等式g(x)<0的解集;
(2)若对一切x>5,均有f(x)≥(m+2)x﹣m﹣15成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】是否存在同时满足下列两条件的直线l:l与抛物线y2=8x有两个不同的交点A和B;线段AB被直线l1:x+5y﹣5=0垂直平分.若不存在,说明理由,若存在,求出直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设AB=ykm,并在公路北侧建造边长为xkm的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且∠ABC=60°。 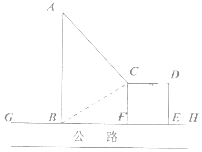
(1)求y关于x的函数解析式,并求出定义域;
(2)如果中转站四堵围墙造价为10万元/km,两条道路造价为30万元/km,问:x取何值时,该公司建设中转站围墙和两条道路总造价M最低.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题.他们在沙滩上画点或用小石子表示数,按照点或小石子能排列的形状对数进行分类.如下图中实心点的个数5,9,14,20,…为梯形数.根据图形的构成,记此数列的第2013项为a2013 , 则a2013﹣5=( ) 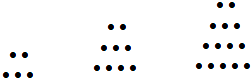
A.2019×2013
B.2019×2012
C.1006×2013
D.2019×1006
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P在直线x+3y﹣2=0上,点Q在直线x+3y+6=0上,线段PQ的中点为M(x0 , y0),且y0<x0+2,则 ![]() 的取值范围是( )
的取值范围是( )
A.[﹣ ![]() ,0)
,0)
B.(﹣ ![]() ,0)
,0)
C.(﹣ ![]() ,+∞)
,+∞)
D.(﹣∞,﹣ ![]() )∪(0,+∞)
)∪(0,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com