
分析 (1)分这名女生来自甲组、来自乙组两种情况,求出好有一名女生的选派方法数.
(2)X的可能取值为0,1,2,3,再求出X取每个值的概率,可得X的概率分布和数学期望.
解答 (1)选出的4名选手中恰好有一名女生的选派方法数为${C}_{2}^{1}$•${C}_{3}^{1}$•${C}_{3}^{2}$+${C}_{2}^{2}$•${C}_{3}^{1}$•${C}_{1}^{1}$=21 种.
(2)X的可能取值为0,1,2,3. $P(X=0)=\frac{C_3^2}{C_5^2C_4^2}=\frac{3}{10×6}=\frac{1}{20}$,$P(X=1)=\frac{C_2^1C_3^1C_3^2+C_3^1}{C_5^2C_4^2}=\frac{2×3×3+3}{10×6}=\frac{7}{20}$,
$P(X=3)=\frac{C_3^2C_3^1}{C_5^2C_4^2}=\frac{3×3}{10×6}=\frac{3}{20}$,P(X=2)=1-P(X=0)-P(X=1)-P(X=3)=$\frac{9}{20}$,故X的概率分布为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{20}$ | $\frac{7}{20}$ | $\frac{9}{20}$ | $\frac{3}{20}$ |
点评 本题主要考查排列组合问题,离散型随机变量的分布列与期望,属于中档题.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [3,5] | B. | [9,25] | C. | $[\frac{12}{5},5]$ | D. | $[\frac{144}{25},25]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
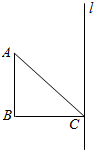 如图,三角形ABC是等腰直角三角形,∠B=90°,AB=1,直线l经过点C且与AB平行,将三角形ABC绕直线l旋转一周得到一个几何体.
如图,三角形ABC是等腰直角三角形,∠B=90°,AB=1,直线l经过点C且与AB平行,将三角形ABC绕直线l旋转一周得到一个几何体.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | [-2,1] | C. | (0,1) | D. | (0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com