
���� ��1�����������x=$\sqrt{a}$ʱ��yȡ��Сֵ$\sqrt{6}$���������a��ֵ���ɣ�
��2���Ƚ�����f��x�����Σ��Ӷ���������ĵ�����������ֵ����Сֵ���������������ֵ��
��3���ֱ����f��x����g��x����ֵ������ת��Ϊ[4��5]⊆[-1-2c��-2c]���õ�����ʽ�飬������ɣ�
��� �⣺��1��������$��{0��\sqrt{a}}]$���Ǽ���������$[{\sqrt{a}��+��}��$������������
��x=$\sqrt{a}$ʱ��y��С����y����Сֵ��2$\sqrt{a}$=$\sqrt{6}$����ã�a=$\frac{3}{2}$��
��2��f��x��=$\frac{{{x^2}+2x+5}}{x+1}$=��x+1��+$\frac{4}{x+1}$��4�����ҽ���x=1ʱ��=��������
�ຯ��f��x����[0��1���ݼ����ڣ�1��2]������
��f��x����Сֵ=f��1��=4��f��x�����ֵ=f��0��=5��
�ຯ����ֵ����[4��5]��
��3����g��x����[0��1]�����ݼ�����g��x����[-1-2c��-2c]��
������֪��[4��5]⊆[-1-2c��-2c]
�����У�$\left\{\begin{array}{l}{-1-2c��4}\\{-2c��5}\end{array}\right.$����ã�c=-$\frac{5}{2}$��
���� ���⿼���ˡ�˫������������y=x+$\frac{a}{x}$��x��0�����ʼ���Ӧ�á����������ĵȼ�ת���Ȼ���֪ʶ��������ܷ����������˷�������ͽ������������������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $x=-\frac{��}{2}$ | B�� | $x=-\frac{��}{4}$ | C�� | $x=-\frac{��}{8}$ | D�� | $x=\frac{5}{4}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��+�ޣ� | B�� | $��{\frac{3}{2}��+��}��$ | C�� | $[{\frac{3}{2}��3}��$ | D�� | ��1��3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
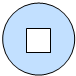 ŷ���ޡ������̡���д���������̣���ȡһ��«���ڵأ���Ǯ����ڣ������������֮����Ǯ���룬��Ǯ��ʪ�����ɼ������г�״Ԫ���������̵ļ�������̾Ϊ��ֹ������ͼͭǮ��ֱ��Ϊ4cm��Բ�Σ����м��б߳�Ϊ1cm�������οף��������ͭǮ�ϵ�һ���ͣ��͵���ֱ��Ϊ0.2cm�����ǡ��͵β����߽硱Ϊ�¼�A�����͵���������������С�Ϊ�¼�B����P��B|A��=$\frac{64}{361��}$����������ֵ���㣩��
ŷ���ޡ������̡���д���������̣���ȡһ��«���ڵأ���Ǯ����ڣ������������֮����Ǯ���룬��Ǯ��ʪ�����ɼ������г�״Ԫ���������̵ļ�������̾Ϊ��ֹ������ͼͭǮ��ֱ��Ϊ4cm��Բ�Σ����м��б߳�Ϊ1cm�������οף��������ͭǮ�ϵ�һ���ͣ��͵���ֱ��Ϊ0.2cm�����ǡ��͵β����߽硱Ϊ�¼�A�����͵���������������С�Ϊ�¼�B����P��B|A��=$\frac{64}{361��}$����������ֵ���㣩���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 25 | B�� | 7 | C�� | 5 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com