已知y=2cos2x+4asinx+a-3
(1)求函数最大值M(a)的表达式.
(2)若f(x)=0在[0,π]有2个解,求a的取值范围.
解:(1)y=2cos
2x+4asinx+a-3=2a
2+a-1-2(sinx-a)
2,当-1≤a≤1时,函数最大值M(a)=2a
2+a-1.
当 a<-1时,函数最大值M(a)=2a
2+a-1-2 (-1-a)
2=-3a-3.
当 a>1时,函数最大值M(a)=2a
2+a-1-2 (1-a)
2=5a-3.
(2)若f(x)=0在[0,π]上有2个解,令 sinx=t,∵0≤x≤π,∴0≤sinx≤1,∴0≤t≤1.
由于当t在[0,1)上任意取一个值,x在[0,π)]上都有2个值与之对应,而当t=1时,只有一个x=

与之对应.
故由题意f(x)=0在[0,π]有2个解,可得关于t的函数 g(t)=2a
2+a-1-2(t-a)
2 =-2t
2+4at+a-1
的图象在[0,1)上,与横轴只能有一个交点,
即关于t的方程 g(t)=0在[0,1)上有唯一解.
∴
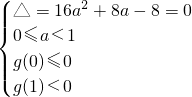
,即
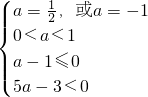
,∴a=

,
故a的取值范围是 {

}.
分析:(1)y=2cos
2x+4asinx+a-3=2a
2+a-1-2(sinx-a)
2,当-1≤a≤1时,函数最大值M(a)=2a
2+a-1,当a<-1时,函数最大值M(a)=2a
2+a-1-2 (-1-a)
2=-3a-3; 当a>1时,函数最大值M(a)=2a
2+a-1-2 (1-a)
2=5a-3.
(2)令 sinx=t,由0≤x≤π,得0≤sinx≤1,由题意可得g(t)=2a
2+a-1-2(t-a)
2,的图象在[0,1)上与横轴
只有一个交点,故有
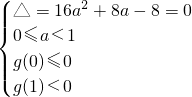
,解不等式求得a的取值范围.
点评:本题考查同角三角函数的基本关系,二次函数的最值问题,令 sinx=t,判断g(t)=2a
2+a-1-2(t-a)
2,在[0,1]上,与横轴有两个交点,是解题的关键.

 与之对应.
与之对应.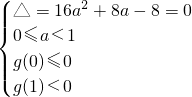 ,即
,即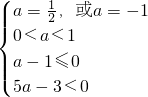 ,∴a=
,∴a= ,
, }.
}.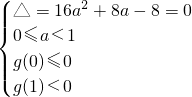 ,解不等式求得a的取值范围.
,解不等式求得a的取值范围.
