
已知袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球 个。若从袋子中随机抽取1个小球,取到标号为2的小球的概率为
个。若从袋子中随机抽取1个小球,取到标号为2的小球的概率为 。
。
(1)求 的值;
的值;
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球的标号为 ,第二次取出的小球的标号为
,第二次取出的小球的标号为 。
。
①记“ ”为事件
”为事件 ,求事件
,求事件 的概率;
的概率;
②在区间 内任取2个实数
内任取2个实数 ,求时间“
,求时间“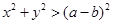 恒成立”的概率.
恒成立”的概率.
(1) ;(2)①
;(2)①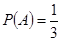 ;②
;②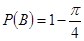 .
.
解析试题分析:(1)古典概型的概率问题,关键是正确找出基本事件总数和所求事件包含的基本事件数,然后利用古典概型的概率计算公式计算;(2)当基本事件总数较少时,用列举法把所有的基本事件一一列举出来,要做到不重不漏,有时可借助列表,树状图列举,当基本事件总数较多时,注意去分排列与组合;(3)注意判断是古典概型还是几何概型,基本事件前者是有限的,后者是无限的,两者都是等可能性.(4)在几何概型中注意区域是线段,平面图形,立体图形.
试题解析:解:(1)由题意,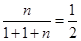 ,
,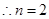
(2)①将标号为2的小球记为 ,
,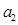 ,两次不放回的取小球的所有基本为:
,两次不放回的取小球的所有基本为:
(0,1),(0,  ),(0,
),(0, 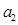 ),(1,0),(1,
),(1,0),(1,  ),
),
(1, 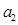 ),(
),( ,0),(
,0),(  ,1),(
,1),(  ,
,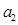 ),(
),(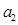 ,0),(
,0),( 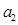 ,1),(
,1),(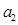 ,
, ),共12个事件A包含的基本事件为: (0,
),共12个事件A包含的基本事件为: (0,  ),(0,
),(0, 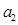 ),(
),( ,0), (
,0), (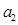 ,0).
,0). 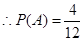
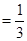
②.事件B等价于: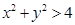 ,
,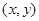 可以看作平面中的点,则全部结果所构成的区域
可以看作平面中的点,则全部结果所构成的区域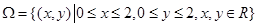 ,
,
而事件B的所构成的区域
B=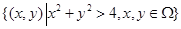 ,
, .
.
考点:(1)古典概型的概率计算;(2)几何概型的概率计算.


科目:高中数学 来源:2015届内蒙古包头市高二下学期期中Ⅰ理科数学试卷(解析版) 题型:解答题
已知函数
(1)若 ,试确定函数
,试确定函数 的单调区间;
的单调区间;
(2)若 ,且对于任意
,且对于任意 ,
, 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com